A Bayesian Unification of Self-Supervised Clustering and Energy-Based Models

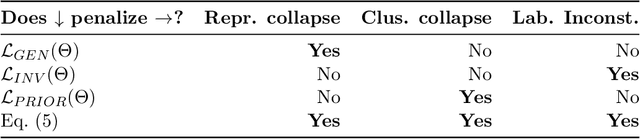
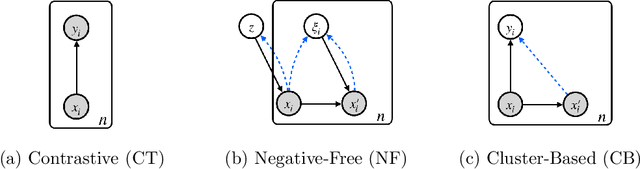
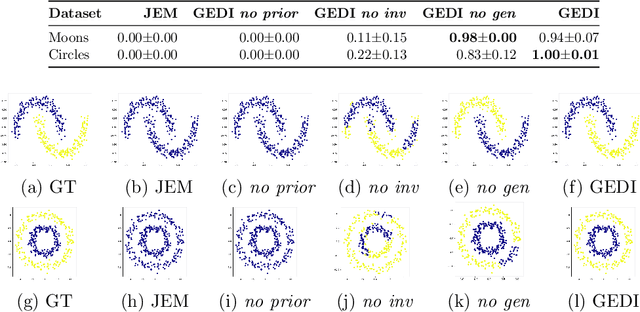
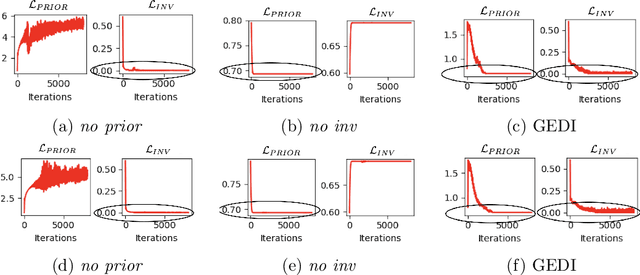
Self-supervised learning is a popular and powerful method for utilizing large amounts of unlabeled data, for which a wide variety of training objectives have been proposed in the literature. In this study, we perform a Bayesian analysis of state-of-the-art self-supervised learning objectives, elucidating the underlying probabilistic graphical models in each class and presenting a standardized methodology for their derivation from first principles. The analysis also indicates a natural means of integrating self-supervised learning with likelihood-based generative models. We instantiate this concept within the realm of cluster-based self-supervised learning and energy models, introducing a novel lower bound which is proven to reliably penalize the most important failure modes. Furthermore, this newly proposed lower bound enables the training of a standard backbone architecture without the necessity for asymmetric elements such as stop gradients, momentum encoders, or specialized clustering layers - typically introduced to avoid learning trivial solutions. Our theoretical findings are substantiated through experiments on synthetic and real-world data, including SVHN, CIFAR10, and CIFAR100, thus showing that our objective function allows to outperform existing self-supervised learning strategies in terms of clustering, generation and out-of-distribution detection performance by a wide margin. We also demonstrate that GEDI can be integrated into a neural-symbolic framework to mitigate the reasoning shortcut problem and to learn higher quality symbolic representations thanks to the enhanced classification performance.