End-to-end localized deep learning for Cryo-ET

Cryo-electron tomography (cryo-ET) enables 3D visualization of cellular environments. Accurate reconstruction of high-resolution volumes is complicated by the very low signal-to-noise ratio and a restricted range of sample tilts, creating a missing wedge of Fourier information. Recent self-supervised deep learning approaches, which post-process initial reconstructions done by filtered backprojection (FBP), have significantly improved reconstruction quality, but they are computationally expensive, demand large memory, and require retraining for each new dataset. End-to-end supervised learning is an appealing alternative but is impeded by the lack of ground truth and the large memory demands of high-resolution volumetric data. Training on synthetic data often leads to overfitting and poor generalization to real data, and, to date, no general end-to-end deep learning reconstructors exist for cryo-ET. In this work, we introduce CryoLithe, a local, memory-efficient reconstruction network that directly estimates the volume from an aligned tilt-series, overcoming the suboptimal FBP. We demonstrate that leveraging transform-domain locality makes our network robust to distribution shifts, enabling effective supervised training and giving excellent results on real data -- without retraining or fine-tuning.

Ice-Tide: Implicit Cryo-ET Imaging and Deformation Estimation

We introduce ICE-TIDE, a method for cryogenic electron tomography (cryo-ET) that simultaneously aligns observations and reconstructs a high-resolution volume. The alignment of tilt series in cryo-ET is a major problem limiting the resolution of reconstructions. ICE-TIDE relies on an efficient coordinate-based implicit neural representation of the volume which enables it to directly parameterize deformations and align the projections. Furthermore, the implicit network acts as an effective regularizer, allowing for high-quality reconstruction at low signal-to-noise ratios as well as partially restoring the missing wedge information. We compare the performance of ICE-TIDE to existing approaches on realistic simulated volumes where the significant gains in resolution and accuracy of recovering deformations can be precisely evaluated. Finally, we demonstrate ICE-TIDE's ability to perform on experimental data sets.

GLIMPSE: Generalized Local Imaging with MLPs

Deep learning is the current de facto state of the art in tomographic imaging. A common approach is to feed the result of a simple inversion, for example the backprojection, to a convolutional neural network (CNN) which then computes the reconstruction. Despite strong results on 'in-distribution' test data similar to the training data, backprojection from sparse-view data delocalizes singularities, so these approaches require a large receptive field to perform well. As a consequence, they overfit to certain global structures which leads to poor generalization on out-of-distribution (OOD) samples. Moreover, their memory complexity and training time scale unfavorably with image resolution, making them impractical for application at realistic clinical resolutions, especially in 3D: a standard U-Net requires a substantial 140GB of memory and 2600 seconds per epoch on a research-grade GPU when training on 1024x1024 images. In this paper, we introduce GLIMPSE, a local processing neural network for computed tomography which reconstructs a pixel value by feeding only the measurements associated with the neighborhood of the pixel to a simple MLP. While achieving comparable or better performance with successful CNNs like the U-Net on in-distribution test data, GLIMPSE significantly outperforms them on OOD samples while maintaining a memory footprint almost independent of image resolution; 5GB memory suffices to train on 1024x1024 images. Further, we built GLIMPSE to be fully differentiable, which enables feats such as recovery of accurate projection angles if they are out of calibration.

Implicit Reconstructions from Deformed Projections for CryoET

Cryo-electron tomography (cryoET) is a technique that captures images of biological samples at different tilts, preserving their native state as much as possible. Along with the partial tilt series and noise, one of the major challenges in estimating the accurate 3D structure of the sample is the deformations in the images incurred during the acquisition. We model these deformations as continuous operators and estimate the unknown 3D volume using implicit neural representations. This framework allows to easily incorporate the deformation and estimate jointly the deformation parameters and the volume using a standard optimization algorithm. This approach doesn't require training data and can benefit from standard prior in the optimization procedure.

FunkNN: Neural Interpolation for Functional Generation

Can we build continuous generative models which generalize across scales, can be evaluated at any coordinate, admit calculation of exact derivatives, and are conceptually simple? Existing MLP-based architectures generate worse samples than the grid-based generators with favorable convolutional inductive biases. Models that focus on generating images at different scales do better, but employ complex architectures not designed for continuous evaluation of images and derivatives. We take a signal-processing perspective and treat continuous image generation as interpolation from samples. Indeed, correctly sampled discrete images contain all information about the low spatial frequencies. The question is then how to extrapolate the spectrum in a data-driven way while meeting the above design criteria. Our answer is FunkNN -- a new convolutional network which learns how to reconstruct continuous images at arbitrary coordinates and can be applied to any image dataset. Combined with a discrete generative model it becomes a functional generator which can act as a prior in continuous ill-posed inverse problems. We show that FunkNN generates high-quality continuous images and exhibits strong out-of-distribution performance thanks to its patch-based design. We further showcase its performance in several stylized inverse problems with exact spatial derivatives.

Joint Cryo-ET Alignment and Reconstruction with Neural Deformation Fields

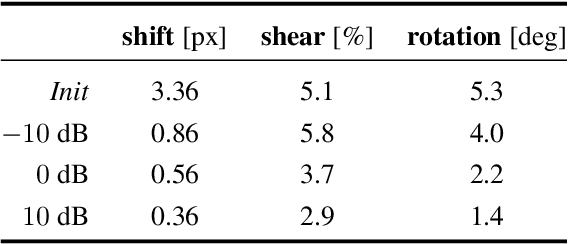
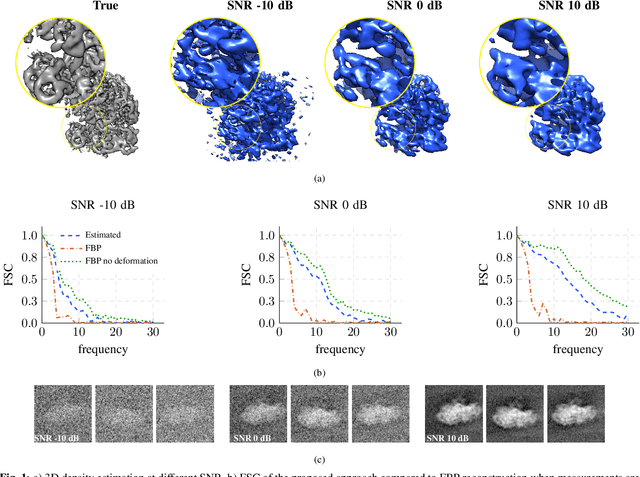
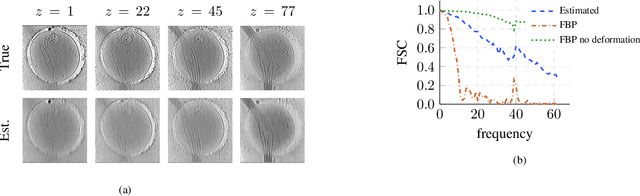
We propose a framework to jointly determine the deformation parameters and reconstruct the unknown volume in electron cryotomography (CryoET). CryoET aims to reconstruct three-dimensional biological samples from two-dimensional projections. A major challenge is that we can only acquire projections for a limited range of tilts, and that each projection undergoes an unknown deformation during acquisition. Not accounting for these deformations results in poor reconstruction. The existing CryoET software packages attempt to align the projections, often in a workflow which uses manual feedback. Our proposed method sidesteps this inconvenience by automatically computing a set of undeformed projections while simultaneously reconstructing the unknown volume. We achieve this by learning a continuous representation of the undeformed measurements and deformation parameters. We show that our approach enables the recovery of high-frequency details that are destroyed without accounting for deformations.

Differentiable Uncalibrated Imaging

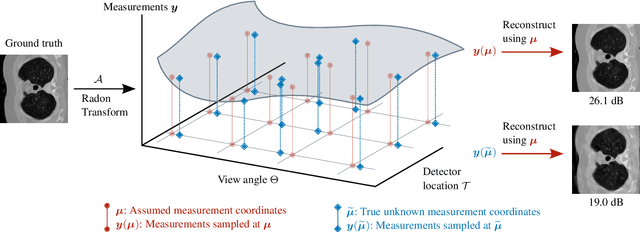
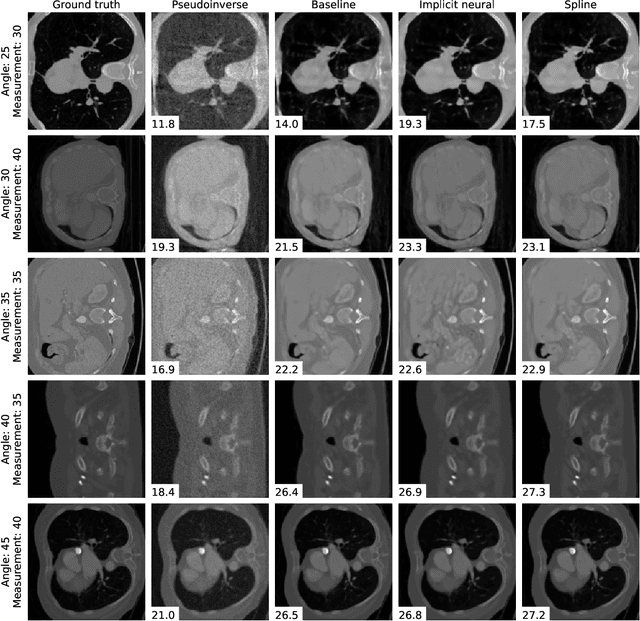
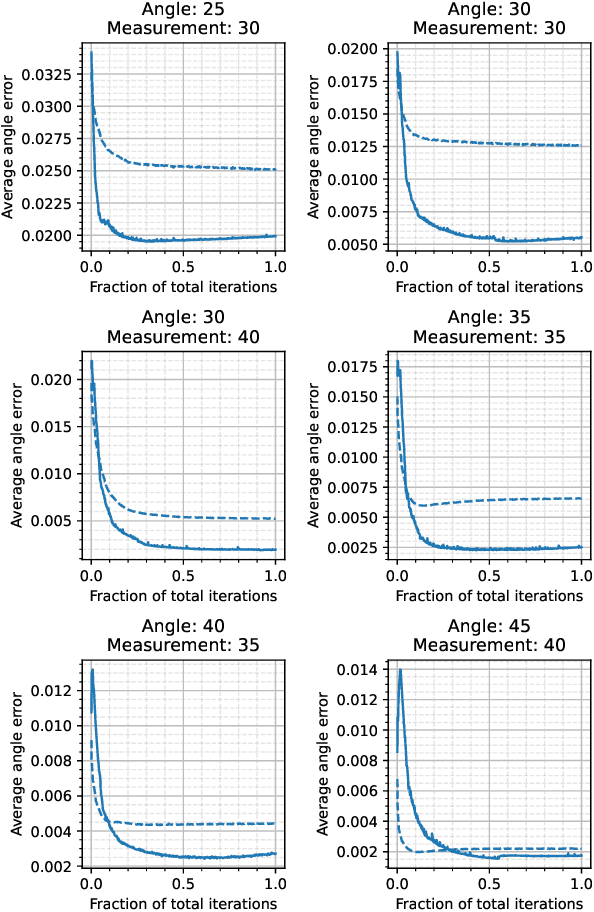
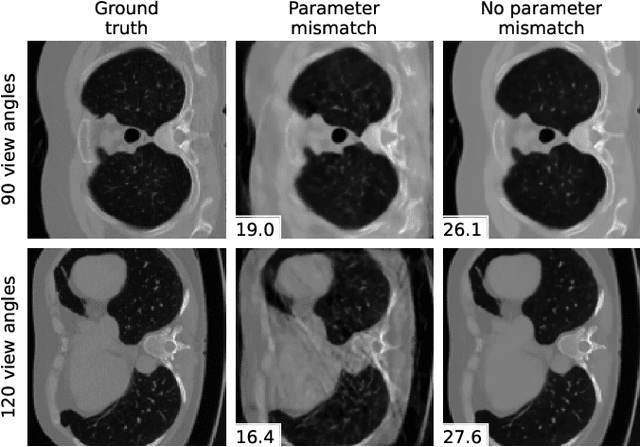
We propose a differentiable imaging framework to address uncertainty in measurement coordinates such as sensor locations and projection angles. We formulate the problem as measurement interpolation at unknown nodes supervised through the forward operator. To solve it we apply implicit neural networks, also known as neural fields, which are naturally differentiable with respect to the input coordinates. We also develop differentiable spline interpolators which perform as well as neural networks, require less time to optimize and have well-understood properties. Differentiability is key as it allows us to jointly fit a measurement representation, optimize over the uncertain measurement coordinates, and perform image reconstruction which in turn ensures consistent calibration. We apply our approach to 2D and 3D computed tomography and show that it produces improved reconstructions compared to baselines that do not account for the lack of calibration. The flexibility of the proposed framework makes it easy to apply to almost arbitrary imaging problems.

Small Transformers Compute Universal Metric Embeddings

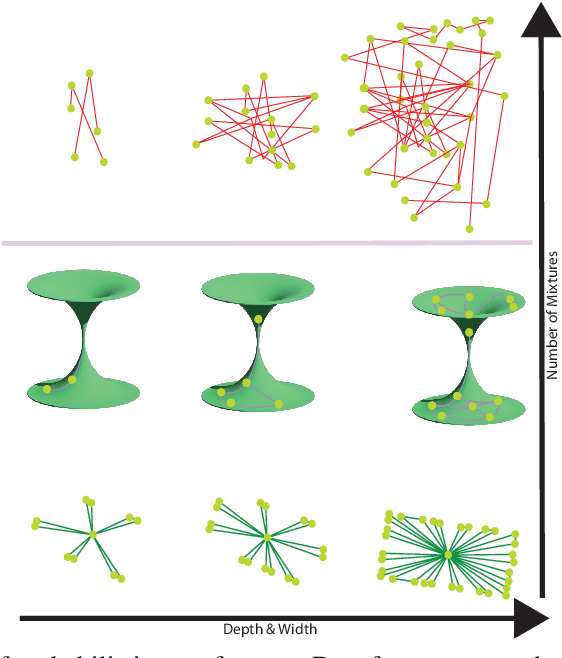
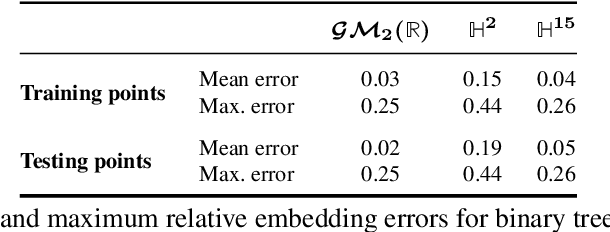
We study representations of data from an arbitrary metric space $\mathcal{X}$ in the space of univariate Gaussian mixtures with a transport metric (Delon and Desolneux 2020). We derive embedding guarantees for feature maps implemented by small neural networks called \emph{probabilistic transformers}. Our guarantees are of memorization type: we prove that a probabilistic transformer of depth about $n\log(n)$ and width about $n^2$ can bi-H\"{o}lder embed any $n$-point dataset from $\mathcal{X}$ with low metric distortion, thus avoiding the curse of dimensionality. We further derive probabilistic bi-Lipschitz guarantees which trade off the amount of distortion and the probability that a randomly chosen pair of points embeds with that distortion. If $\mathcal{X}$'s geometry is sufficiently regular, we obtain stronger, bi-Lipschitz guarantees for all points in the dataset. As applications we derive neural embedding guarantees for datasets from Riemannian manifolds, metric trees, and certain types of combinatorial graphs.

Manifold Rewiring for Unlabeled Imaging

Geometric data analysis relies on graphs that are either given as input or inferred from data. These graphs are often treated as "correct" when solving downstream tasks such as graph signal denoising. But real-world graphs are known to contain missing and spurious links. Similarly, graphs inferred from noisy data will be perturbed. We thus define and study the problem of graph denoising, as opposed to graph signal denoising, and propose an approach based on link-prediction graph neural networks. We focus in particular on neighborhood graphs over point clouds sampled from low-dimensional manifolds, such as those arising in imaging inverse problems and exploratory data analysis. We illustrate our graph denoising framework on regular synthetic graphs and then apply it to single-particle cryo-EM where the measurements are corrupted by very high levels of noise. Due to this degradation, the initial graph is contaminated by noise, leading to missing or spurious edges. We show that our proposed graph denoising algorithm improves the state-of-the-art performance of multi-frequency vector diffusion maps.

Blind inverse problems with isolated spikes

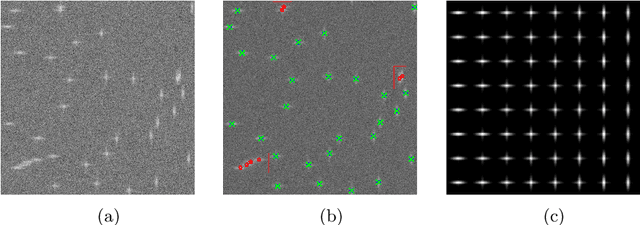
Assume that an unknown integral operator living in some known subspace is observed indirectly, by evaluating its action on a few Dirac masses at unknown locations. Is this information enough to recover the operator and the impulse responses locations stably? We study this question and answer positively under realistic technical assumptions. We illustrate the well-foundedness of this theory on two challenging optical imaging problems: blind super-resolution and deconvolution. This provides a simple, practical and theoretically grounded approach to solve these long resisting problems.