Bayesian Optimization of Sampling Densities in MRI

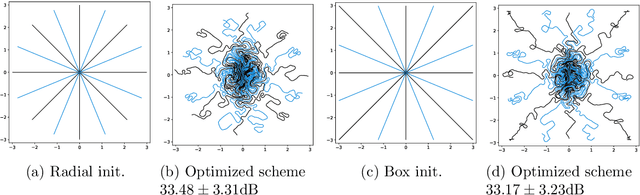
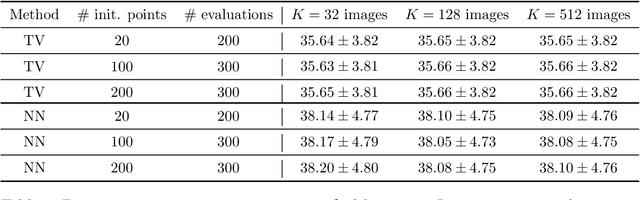
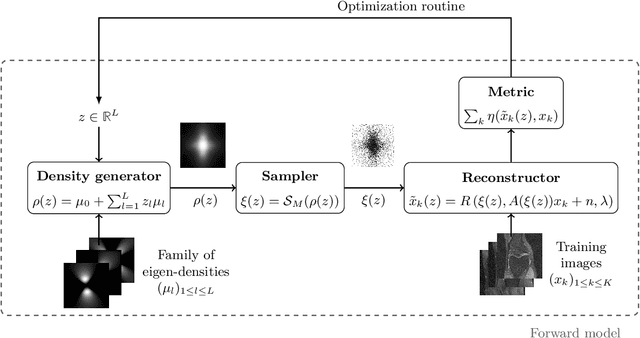
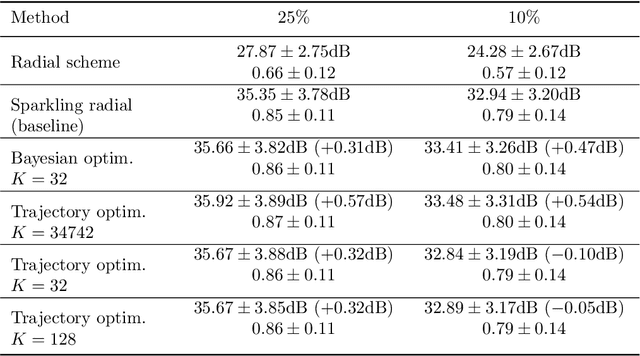
Data-driven optimization of sampling patterns in MRI has recently received a significant attention. Following recent observations on the combinatorial number of minimizers in off-the-grid optimization, we propose a framework to globally optimize the sampling densities using Bayesian optimization. Using a dimension reduction technique, we optimize the sampling trajectories more than 20 times faster than conventional off-the-grid methods, with a restricted number of training samples. This method -- among other benefits -- discards the need of automatic differentiation. Its performance is slightly worse than state-of-the-art learned trajectories since it reduces the space of admissible trajectories, but comes with significant computational advantages. Other contributions include: i) a careful evaluation of the distance in probability space to generate trajectories ii) a specific training procedure on families of operators for unrolled reconstruction networks and iii) a gradient projection based scheme for trajectory optimization.

Training Adaptive Reconstruction Networks for Inverse Problems

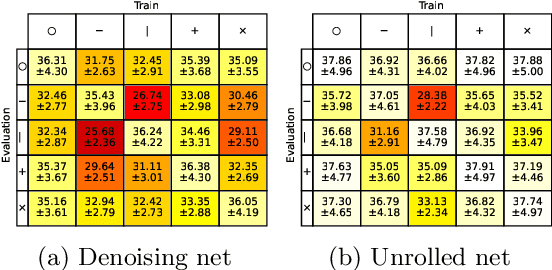
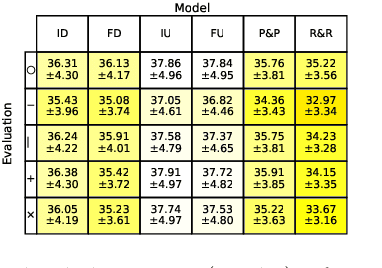
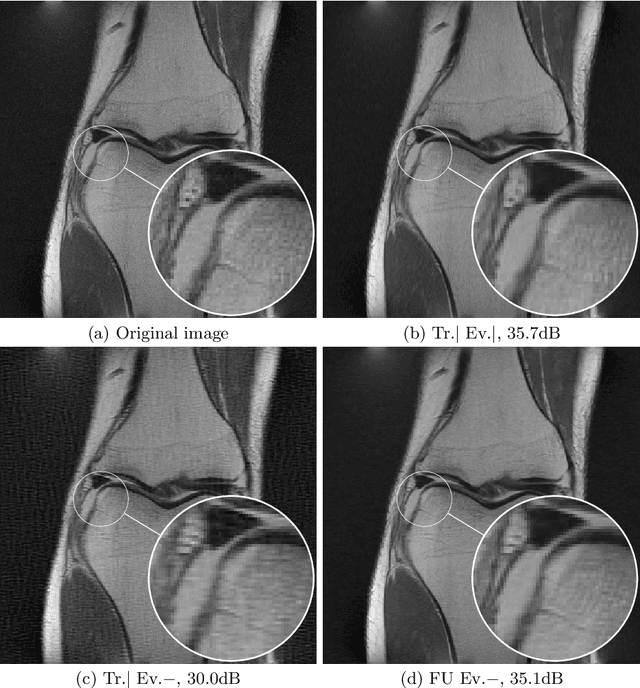
Neural networks are full of promises for the resolution of ill-posed inverse problems. In particular, physics informed learning approaches already seem to progressively gradually replace carefully hand-crafted reconstruction algorithms, for their superior quality. The aim of this paper is twofold. First we show a significant weakness of these networks: they do not adapt efficiently to variations of the forward model. Second, we show that training the network with a family of forward operators allows to solve the adaptivity problem without compromising the reconstruction quality significantly. All our experiments are carefully devised on partial Fourier sampling problems arising in magnetic resonance imaging (MRI).

Blind inverse problems with isolated spikes

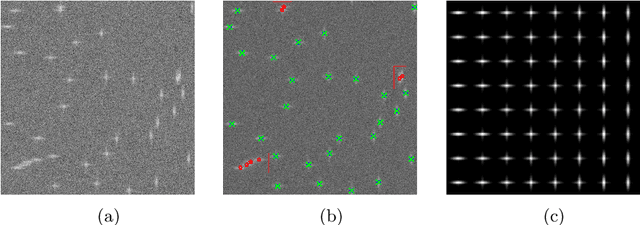
Assume that an unknown integral operator living in some known subspace is observed indirectly, by evaluating its action on a few Dirac masses at unknown locations. Is this information enough to recover the operator and the impulse responses locations stably? We study this question and answer positively under realistic technical assumptions. We illustrate the well-foundedness of this theory on two challenging optical imaging problems: blind super-resolution and deconvolution. This provides a simple, practical and theoretically grounded approach to solve these long resisting problems.

Off-the-grid data-driven optimization of sampling schemes in MRI

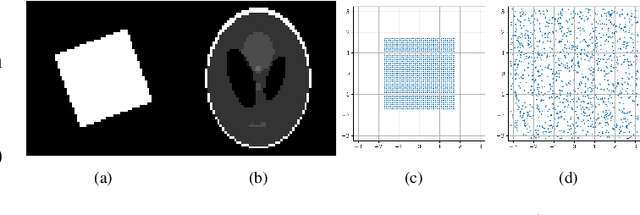
We propose a novel learning based algorithm to generate efficient and physically plausible sampling patterns in MRI. This method has a few advantages compared to recent learning based approaches: i) it works off-the-grid and ii) allows to handle arbitrary physical constraints. These two features allow for much more versatility in the sampling patterns that can take advantage of all the degrees of freedom offered by an MRI scanner. The method consists in a high dimensional optimization of a cost function defined implicitly by an algorithm. We propose various numerical tools to address this numerical challenge.

Hyperspectral pan-sharpening: a variational convex constrained formulation to impose parallel level lines, solved with ADMM

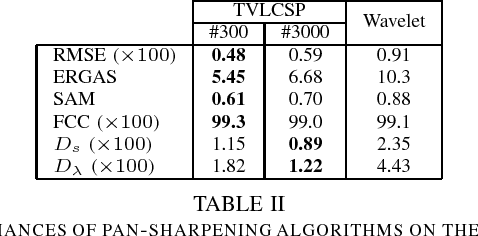
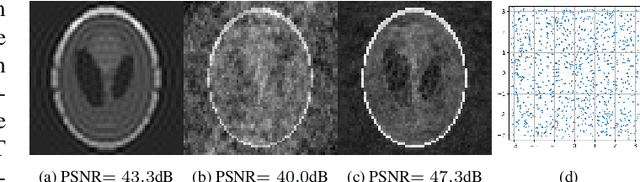
In this paper, we address the issue of hyperspectral pan-sharpening, which consists in fusing a (low spatial resolution) hyperspectral image HX and a (high spatial resolution) panchromatic image P to obtain a high spatial resolution hyperspectral image. The problem is addressed under a variational convex constrained formulation. The objective favors high resolution spectral bands with level lines parallel to those of the panchromatic image. This term is balanced with a total variation term as regularizer. Fit-to-P data and fit-to-HX data constraints are effectively considered as mathematical constraints, which depend on the statistics of the data noise measurements. The developed Alternating Direction Method of Multipliers (ADMM) optimization scheme enables us to solve this problem efficiently despite the non differentiabilities and the huge number of unknowns.

Processing stationary noise: model and parameter selection in variational methods

Additive or multiplicative stationary noise recently became an important issue in applied fields such as microscopy or satellite imaging. Relatively few works address the design of dedicated denoising methods compared to the usual white noise setting. We recently proposed a variational algorithm to tackle this issue. In this paper, we analyze this problem from a statistical point of view and provide deterministic properties of the solutions of the associated variational problems. In the first part of this work, we demonstrate that in many practical problems, the noise can be assimilated to a colored Gaussian noise. We provide a quantitative measure of the distance between a stationary process and the corresponding Gaussian process. In the second part, we focus on the Gaussian setting and analyze denoising methods which consist of minimizing the sum of a total variation term and an $l^2$ data fidelity term. While the constrained formulation of this problem allows to easily tune the parameters, the Lagrangian formulation can be solved more efficiently since the problem is strongly convex. Our second contribution consists in providing analytical values of the regularization parameter in order to approximately satisfy Morozov's discrepancy principle.

Image restoration using sparse approximations of spatially varying blur operators in the wavelet domain

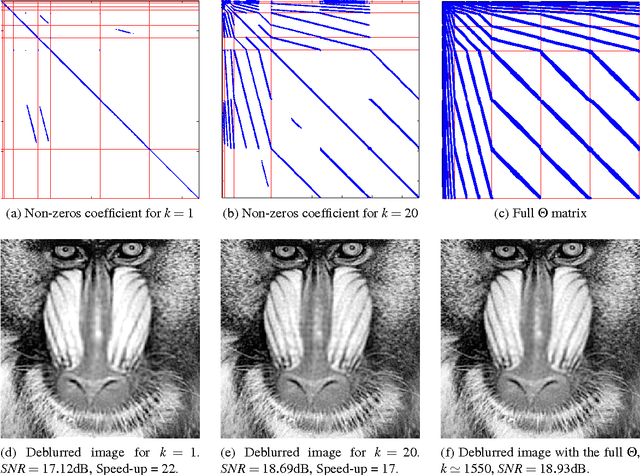
Restoration of images degraded by spatially varying blurs is an issue of increasing importance in the context of photography, satellite or microscopy imaging. One of the main difficulty to solve this problem comes from the huge dimensions of the blur matrix. It prevents the use of naive approaches for performing matrix-vector multiplications. In this paper, we propose to approximate the blur operator by a matrix sparse in the wavelet domain. We justify this approach from a mathematical point of view and investigate the approximation quality numerically. We finish by showing that the sparsity pattern of the matrix can be pre-defined, which is central in tasks such as blind deconvolution.