Bayesian Optimization of Sampling Densities in MRI

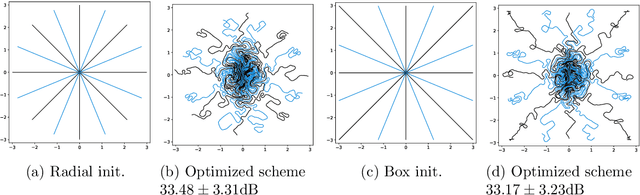
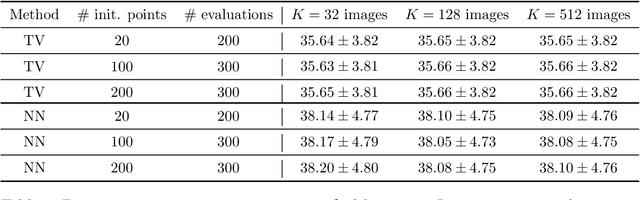
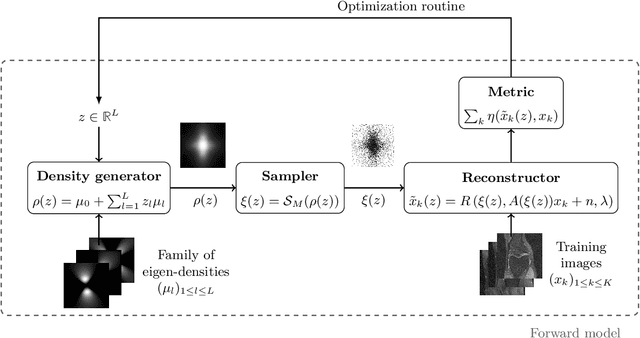
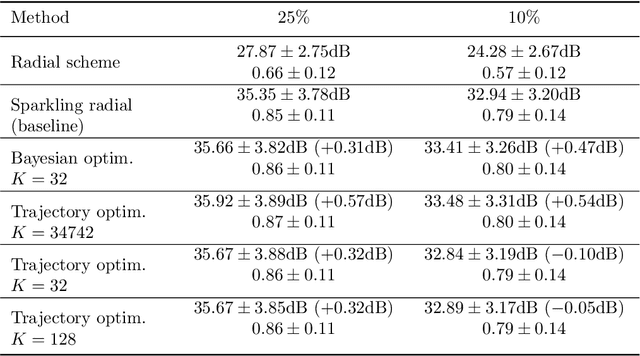
Data-driven optimization of sampling patterns in MRI has recently received a significant attention. Following recent observations on the combinatorial number of minimizers in off-the-grid optimization, we propose a framework to globally optimize the sampling densities using Bayesian optimization. Using a dimension reduction technique, we optimize the sampling trajectories more than 20 times faster than conventional off-the-grid methods, with a restricted number of training samples. This method -- among other benefits -- discards the need of automatic differentiation. Its performance is slightly worse than state-of-the-art learned trajectories since it reduces the space of admissible trajectories, but comes with significant computational advantages. Other contributions include: i) a careful evaluation of the distance in probability space to generate trajectories ii) a specific training procedure on families of operators for unrolled reconstruction networks and iii) a gradient projection based scheme for trajectory optimization.