Adaptive scaling of the learning rate by second order automatic differentiation

In the context of the optimization of Deep Neural Networks, we propose to rescale the learning rate using a new technique of automatic differentiation. This technique relies on the computation of the {\em curvature}, a second order information whose computational complexity is in between the computation of the gradient and the one of the Hessian-vector product. If (1C,1M) represents respectively the computational time and memory footprint of the gradient method, the new technique increase the overall cost to either (1.5C,2M) or (2C,1M). This rescaling has the appealing characteristic of having a natural interpretation, it allows the practitioner to choose between exploration of the parameters set and convergence of the algorithm. The rescaling is adaptive, it depends on the data and on the direction of descent. The numerical experiments highlight the different exploration/convergence regimes.

Bayesian Optimization of Sampling Densities in MRI

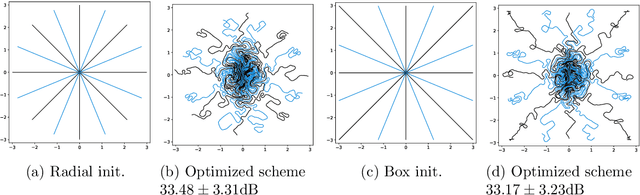
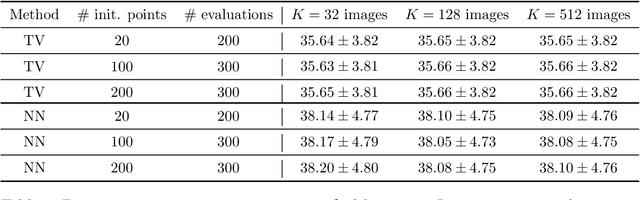
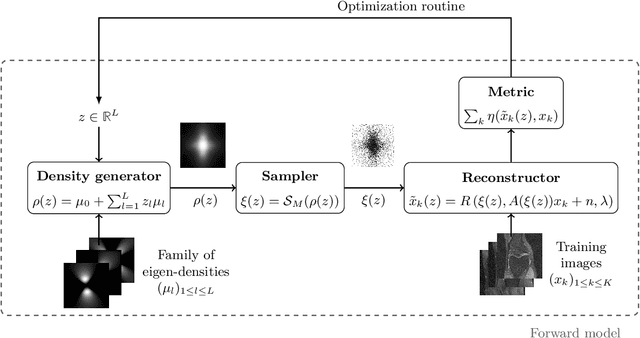
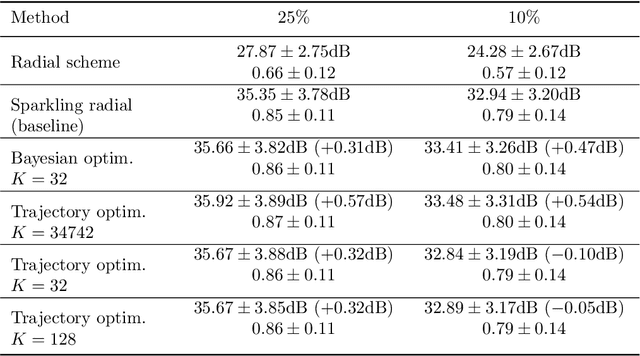
Data-driven optimization of sampling patterns in MRI has recently received a significant attention. Following recent observations on the combinatorial number of minimizers in off-the-grid optimization, we propose a framework to globally optimize the sampling densities using Bayesian optimization. Using a dimension reduction technique, we optimize the sampling trajectories more than 20 times faster than conventional off-the-grid methods, with a restricted number of training samples. This method -- among other benefits -- discards the need of automatic differentiation. Its performance is slightly worse than state-of-the-art learned trajectories since it reduces the space of admissible trajectories, but comes with significant computational advantages. Other contributions include: i) a careful evaluation of the distance in probability space to generate trajectories ii) a specific training procedure on families of operators for unrolled reconstruction networks and iii) a gradient projection based scheme for trajectory optimization.

CorticalFlow: A Diffeomorphic Mesh Deformation Module for Cortical Surface Reconstruction

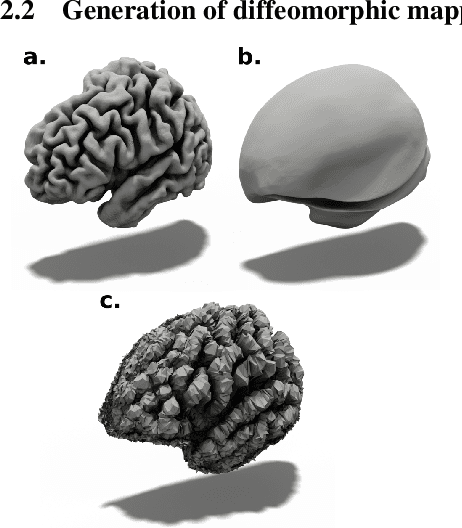
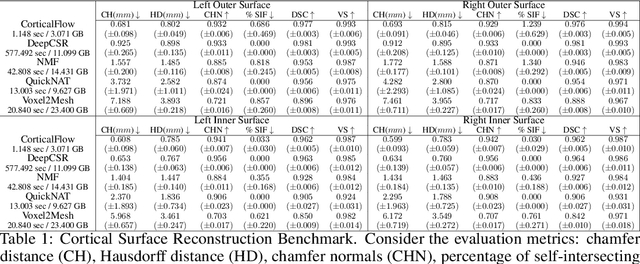
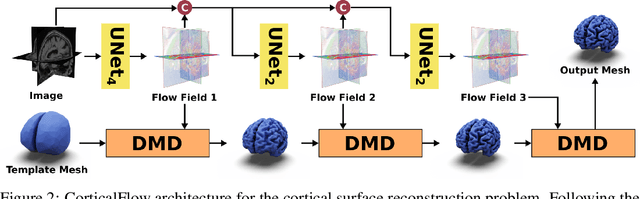
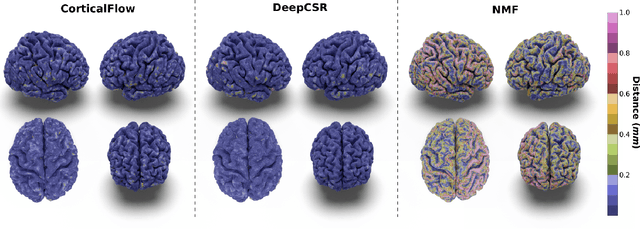
In this paper we introduce CorticalFlow, a new geometric deep-learning model that, given a 3-dimensional image, learns to deform a reference template towards a targeted object. To conserve the template mesh's topological properties, we train our model over a set of diffeomorphic transformations. This new implementation of a flow Ordinary Differential Equation (ODE) framework benefits from a small GPU memory footprint, allowing the generation of surfaces with several hundred thousand vertices. To reduce topological errors introduced by its discrete resolution, we derive numeric conditions which improve the manifoldness of the predicted triangle mesh. To exhibit the utility of CorticalFlow, we demonstrate its performance for the challenging task of brain cortical surface reconstruction. In contrast to current state-of-the-art, CorticalFlow produces superior surfaces while reducing the computation time from nine and a half minutes to one second. More significantly, CorticalFlow enforces the generation of anatomically plausible surfaces; the absence of which has been a major impediment restricting the clinical relevance of such surface reconstruction methods.

Off-the-grid data-driven optimization of sampling schemes in MRI

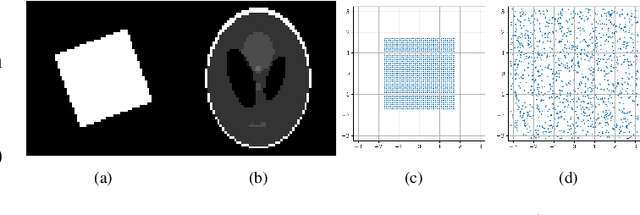
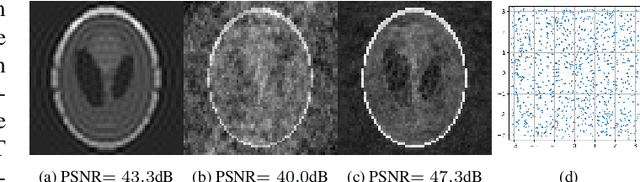
We propose a novel learning based algorithm to generate efficient and physically plausible sampling patterns in MRI. This method has a few advantages compared to recent learning based approaches: i) it works off-the-grid and ii) allows to handle arbitrary physical constraints. These two features allow for much more versatility in the sampling patterns that can take advantage of all the degrees of freedom offered by an MRI scanner. The method consists in a high dimensional optimization of a cost function defined implicitly by an algorithm. We propose various numerical tools to address this numerical challenge.