CorticalFlow$^{++}$: Boosting Cortical Surface Reconstruction Accuracy, Regularity, and Interoperability

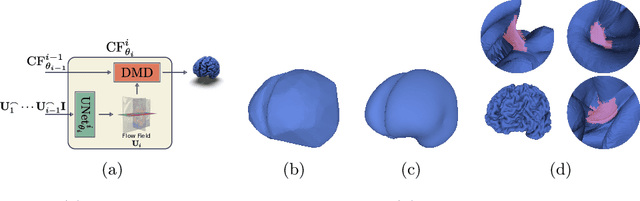
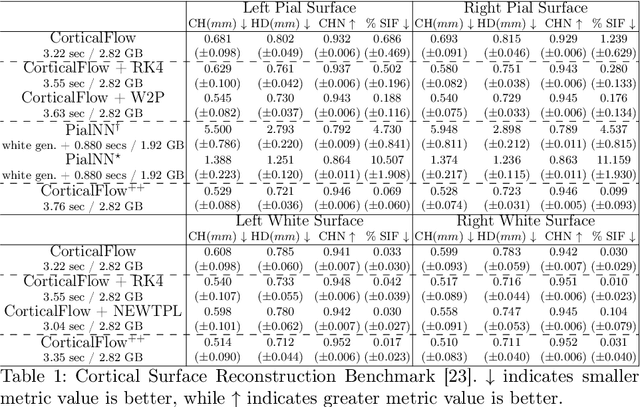
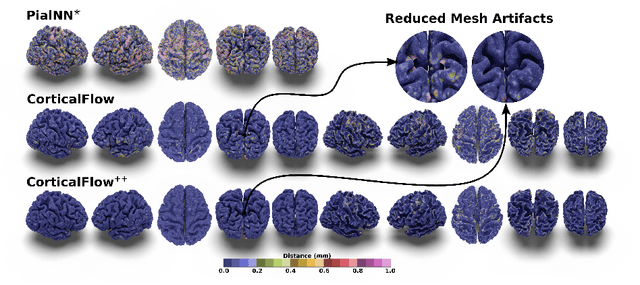
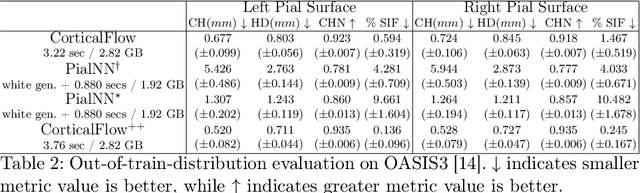
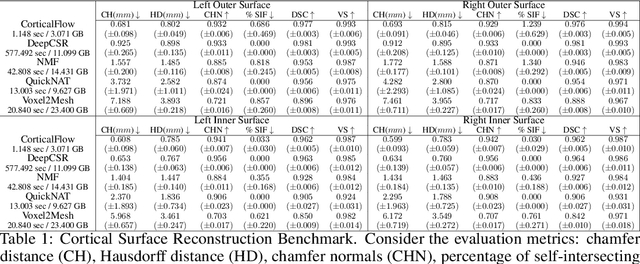
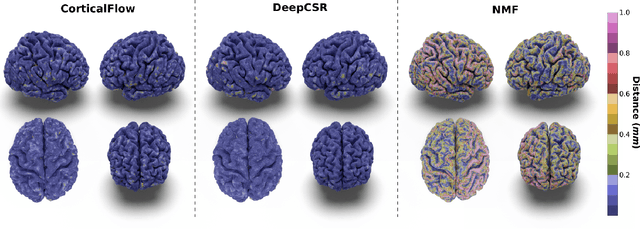
The problem of Cortical Surface Reconstruction from magnetic resonance imaging has been traditionally addressed using lengthy pipelines of image processing techniques like FreeSurfer, CAT, or CIVET. These frameworks require very long runtimes deemed unfeasible for real-time applications and unpractical for large-scale studies. Recently, supervised deep learning approaches have been introduced to speed up this task cutting down the reconstruction time from hours to seconds. Using the state-of-the-art CorticalFlow model as a blueprint, this paper proposes three modifications to improve its accuracy and interoperability with existing surface analysis tools, while not sacrificing its fast inference time and low GPU memory consumption. First, we employ a more accurate ODE solver to reduce the diffeomorphic mapping approximation error. Second, we devise a routine to produce smoother template meshes avoiding mesh artifacts caused by sharp edges in CorticalFlow's convex-hull based template. Last, we recast pial surface prediction as the deformation of the predicted white surface leading to a one-to-one mapping between white and pial surface vertices. This mapping is essential to many existing surface analysis tools for cortical morphometry. We name the resulting method CorticalFlow$^{++}$. Using large-scale datasets, we demonstrate the proposed changes provide more geometric accuracy and surface regularity while keeping the reconstruction time and GPU memory requirements almost unchanged.

CorticalFlow: A Diffeomorphic Mesh Deformation Module for Cortical Surface Reconstruction

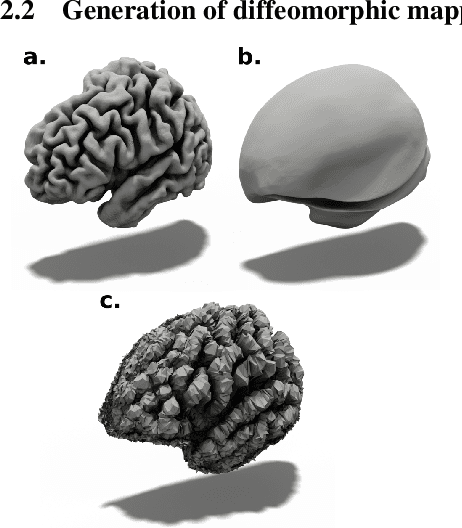
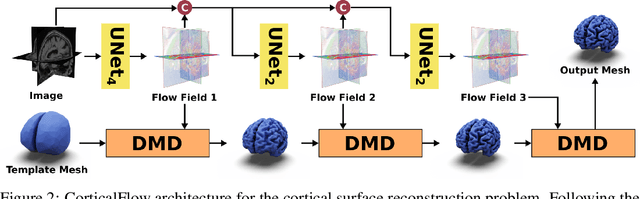
In this paper we introduce CorticalFlow, a new geometric deep-learning model that, given a 3-dimensional image, learns to deform a reference template towards a targeted object. To conserve the template mesh's topological properties, we train our model over a set of diffeomorphic transformations. This new implementation of a flow Ordinary Differential Equation (ODE) framework benefits from a small GPU memory footprint, allowing the generation of surfaces with several hundred thousand vertices. To reduce topological errors introduced by its discrete resolution, we derive numeric conditions which improve the manifoldness of the predicted triangle mesh. To exhibit the utility of CorticalFlow, we demonstrate its performance for the challenging task of brain cortical surface reconstruction. In contrast to current state-of-the-art, CorticalFlow produces superior surfaces while reducing the computation time from nine and a half minutes to one second. More significantly, CorticalFlow enforces the generation of anatomically plausible surfaces; the absence of which has been a major impediment restricting the clinical relevance of such surface reconstruction methods.