Adaptive scaling of the learning rate by second order automatic differentiation

In the context of the optimization of Deep Neural Networks, we propose to rescale the learning rate using a new technique of automatic differentiation. This technique relies on the computation of the {\em curvature}, a second order information whose computational complexity is in between the computation of the gradient and the one of the Hessian-vector product. If (1C,1M) represents respectively the computational time and memory footprint of the gradient method, the new technique increase the overall cost to either (1.5C,2M) or (2C,1M). This rescaling has the appealing characteristic of having a natural interpretation, it allows the practitioner to choose between exploration of the parameters set and convergence of the algorithm. The rescaling is adaptive, it depends on the data and on the direction of descent. The numerical experiments highlight the different exploration/convergence regimes.

Bayesian Optimization of Sampling Densities in MRI

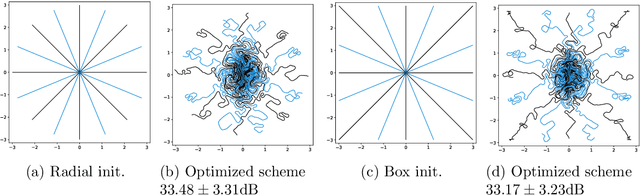
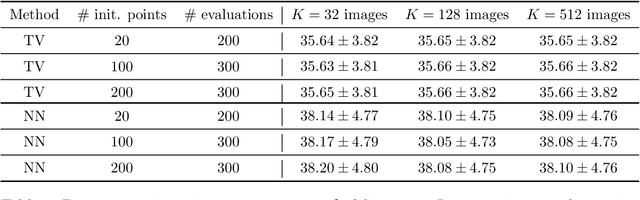
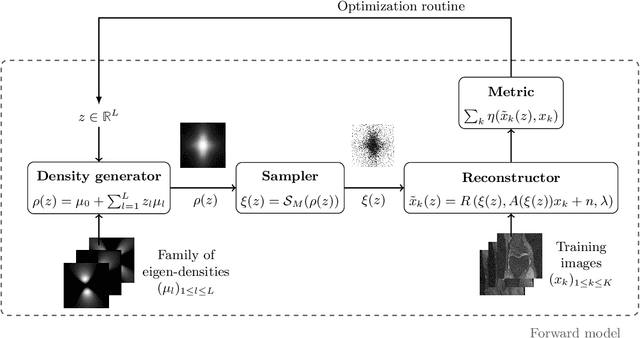
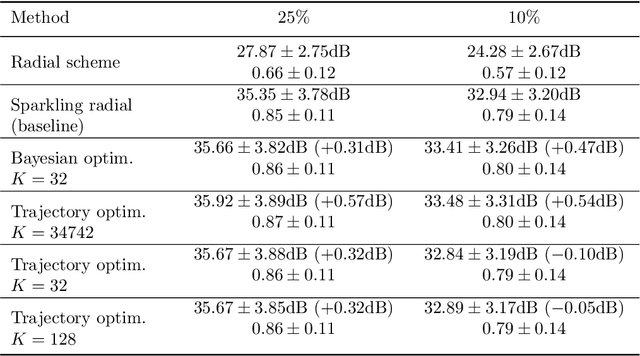
Data-driven optimization of sampling patterns in MRI has recently received a significant attention. Following recent observations on the combinatorial number of minimizers in off-the-grid optimization, we propose a framework to globally optimize the sampling densities using Bayesian optimization. Using a dimension reduction technique, we optimize the sampling trajectories more than 20 times faster than conventional off-the-grid methods, with a restricted number of training samples. This method -- among other benefits -- discards the need of automatic differentiation. Its performance is slightly worse than state-of-the-art learned trajectories since it reduces the space of admissible trajectories, but comes with significant computational advantages. Other contributions include: i) a careful evaluation of the distance in probability space to generate trajectories ii) a specific training procedure on families of operators for unrolled reconstruction networks and iii) a gradient projection based scheme for trajectory optimization.

Training Adaptive Reconstruction Networks for Inverse Problems

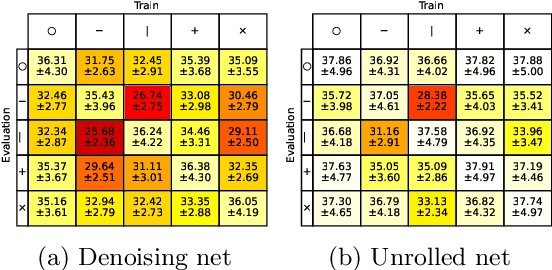
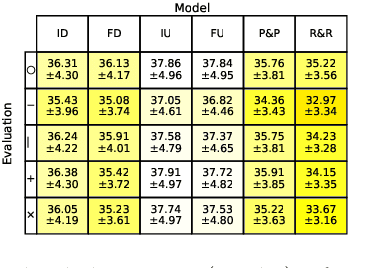
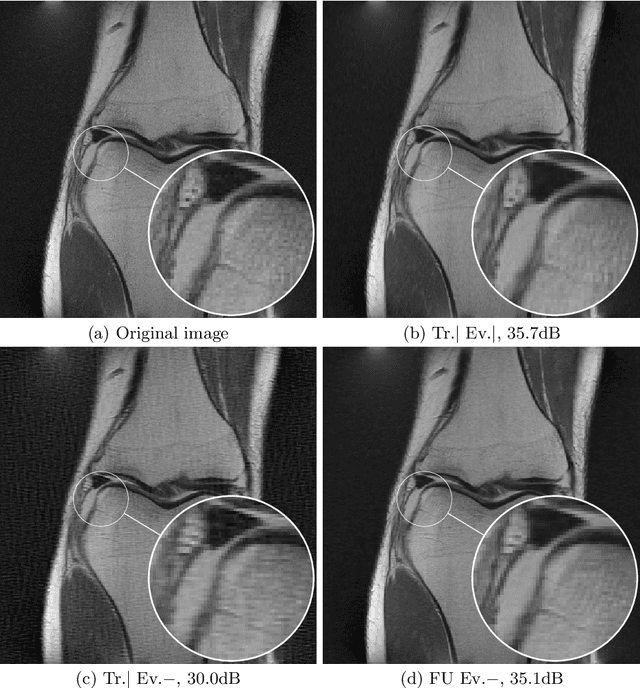
Neural networks are full of promises for the resolution of ill-posed inverse problems. In particular, physics informed learning approaches already seem to progressively gradually replace carefully hand-crafted reconstruction algorithms, for their superior quality. The aim of this paper is twofold. First we show a significant weakness of these networks: they do not adapt efficiently to variations of the forward model. Second, we show that training the network with a family of forward operators allows to solve the adaptivity problem without compromising the reconstruction quality significantly. All our experiments are carefully devised on partial Fourier sampling problems arising in magnetic resonance imaging (MRI).

Off-the-grid data-driven optimization of sampling schemes in MRI

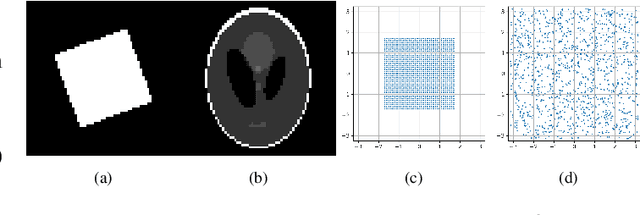
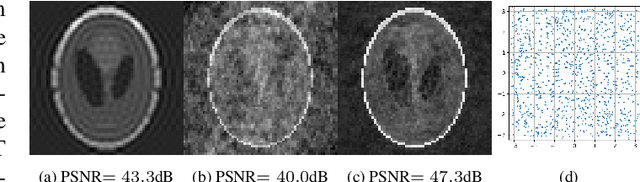
We propose a novel learning based algorithm to generate efficient and physically plausible sampling patterns in MRI. This method has a few advantages compared to recent learning based approaches: i) it works off-the-grid and ii) allows to handle arbitrary physical constraints. These two features allow for much more versatility in the sampling patterns that can take advantage of all the degrees of freedom offered by an MRI scanner. The method consists in a high dimensional optimization of a cost function defined implicitly by an algorithm. We propose various numerical tools to address this numerical challenge.