Image restoration using sparse approximations of spatially varying blur operators in the wavelet domain
Paper and Code
May 30, 2013


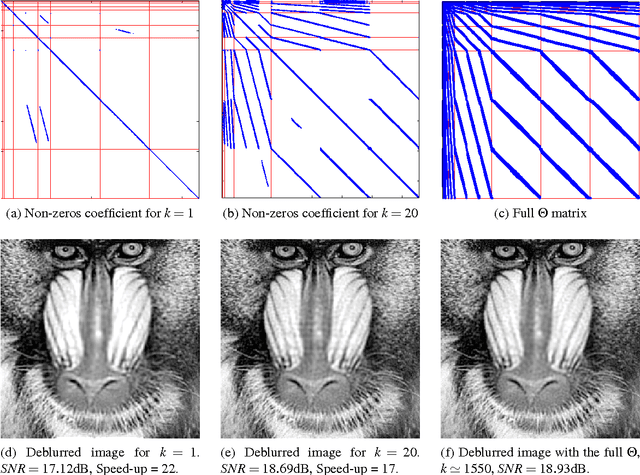
Restoration of images degraded by spatially varying blurs is an issue of increasing importance in the context of photography, satellite or microscopy imaging. One of the main difficulty to solve this problem comes from the huge dimensions of the blur matrix. It prevents the use of naive approaches for performing matrix-vector multiplications. In this paper, we propose to approximate the blur operator by a matrix sparse in the wavelet domain. We justify this approach from a mathematical point of view and investigate the approximation quality numerically. We finish by showing that the sparsity pattern of the matrix can be pre-defined, which is central in tasks such as blind deconvolution.
* 6 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge