Hyperspectral pan-sharpening: a variational convex constrained formulation to impose parallel level lines, solved with ADMM
Paper and Code
May 10, 2014


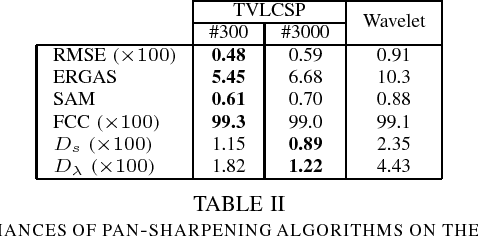
In this paper, we address the issue of hyperspectral pan-sharpening, which consists in fusing a (low spatial resolution) hyperspectral image HX and a (high spatial resolution) panchromatic image P to obtain a high spatial resolution hyperspectral image. The problem is addressed under a variational convex constrained formulation. The objective favors high resolution spectral bands with level lines parallel to those of the panchromatic image. This term is balanced with a total variation term as regularizer. Fit-to-P data and fit-to-HX data constraints are effectively considered as mathematical constraints, which depend on the statistics of the data noise measurements. The developed Alternating Direction Method of Multipliers (ADMM) optimization scheme enables us to solve this problem efficiently despite the non differentiabilities and the huge number of unknowns.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge