Iterated Piecewise Affine (IPA) Approximation for Language Modeling

In this work, we demonstrate the application of a simple first-order Taylor expansion to approximate a generic function $F: R^{n \times m} \to R^{n \times m}$ and utilize it in language modeling. To enhance the basic Taylor expansion, we introduce iteration and piecewise modeling, leading us to name the algorithm the Iterative Piecewise Affine (IPA) approximation. The final algorithm exhibits interesting resemblances to the Transformers decoder architecture. By comparing parameter arrangements in IPA and Transformers, we observe a strikingly similar performance, with IPA outperforming Transformers by 1.5\% in the next token prediction task with cross-entropy loss for smaller sequence lengths.

Convex Risk Bounded Continuous-Time Trajectory Planning and Tube Design in Uncertain Nonconvex Environments

In this paper, we address the trajectory planning problem in uncertain nonconvex static and dynamic environments that contain obstacles with probabilistic location, size, and geometry. To address this problem, we provide a risk bounded trajectory planning method that looks for continuous-time trajectories with guaranteed bounded risk over the planning time horizon. Risk is defined as the probability of collision with uncertain obstacles. Existing approaches to address risk bounded trajectory planning problems either are limited to Gaussian uncertainties and convex obstacles or rely on sampling-based methods that need uncertainty samples and time discretization. To address the risk bounded trajectory planning problem, we leverage the notion of risk contours to transform the risk bounded planning problem into a deterministic optimization problem. Risk contours are the set of all points in the uncertain environment with guaranteed bounded risk. The obtained deterministic optimization is, in general, nonlinear and nonconvex time-varying optimization. We provide convex methods based on sum-of-squares optimization to efficiently solve the obtained nonconvex time-varying optimization problem and obtain the continuous-time risk bounded trajectories without time discretization. The provided approach deals with arbitrary (and known) probabilistic uncertainties, nonconvex and nonlinear, static and dynamic obstacles, and is suitable for online trajectory planning problems. In addition, we provide convex methods based on sum-of-squares optimization to build the max-sized tube with respect to its parameterization along the trajectory so that any state inside the tube is guaranteed to have bounded risk.

LACoS-BLOOM: Low-rank Adaptation with Contrastive objective on 8 bits Siamese-BLOOM

Text embeddings are useful features for several NLP applications, such as sentence similarity, text clustering, and semantic search. In this paper, we present a Low-rank Adaptation with a Contrastive objective on top of 8-bit Siamese-BLOOM, a multilingual large language model optimized to produce semantically meaningful word embeddings. The innovation is threefold. First, we cast BLOOM weights to 8-bit values. Second, we fine-tune BLOOM with a scalable adapter (LoRA) and 8-bit Adam optimizer for sentence similarity classification. Third, we apply a Siamese architecture on BLOOM model with a contrastive objective to ease the multi-lingual labeled data scarcity. The experiment results show the quality of learned embeddings from LACoS-BLOOM is proportional to the number of model parameters and the amount of unlabeled training data. With the parameter efficient fine-tuning design, we are able to run BLOOM 7.1 billion parameters end-to-end on a single GPU machine with 32GB memory. Compared to previous solution Sentence-BERT, we achieve significant improvement on both English and multi-lingual STS tasks.

Non-Gaussian Uncertainty Minimization Based Control of Stochastic Nonlinear Robotic Systems

In this paper, we consider the closed-loop control problem of nonlinear robotic systems in the presence of probabilistic uncertainties and disturbances. More precisely, we design a state feedback controller that minimizes deviations of the states of the system from the nominal state trajectories due to uncertainties and disturbances. Existing approaches to address the control problem of probabilistic systems are limited to particular classes of uncertainties and systems such as Gaussian uncertainties and processes and linearized systems. We present an approach that deals with nonlinear dynamics models and arbitrary known probabilistic uncertainties. We formulate the controller design problem as an optimization problem in terms of statistics of the probability distributions including moments and characteristic functions. In particular, in the provided optimization problem, we use moments and characteristic functions to propagate uncertainties throughout the nonlinear motion model of robotic systems. In order to reduce the tracking deviations, we minimize the uncertainty of the probabilistic states around the nominal trajectory by minimizing the trace and the determinant of the covariance matrix of the probabilistic states. To obtain the state feedback gains, we solve deterministic optimization problems in terms of moments, characteristic functions, and state feedback gains using off-the-shelf interior-point optimization solvers. To illustrate the performance of the proposed method, we compare our method with existing probabilistic control methods.

Real-Time Tube-Based Non-Gaussian Risk Bounded Motion Planning for Stochastic Nonlinear Systems in Uncertain Environments via Motion Primitives

We consider the motion planning problem for stochastic nonlinear systems in uncertain environments. More precisely, in this problem the robot has stochastic nonlinear dynamics and uncertain initial locations, and the environment contains multiple dynamic uncertain obstacles. Obstacles can be of arbitrary shape, can deform, and can move. All uncertainties do not necessarily have Gaussian distribution. This general setting has been considered and solved in [1]. In addition to the assumptions above, in this paper, we consider long-term tasks, where the planning method in [1] would fail, as the uncertainty of the system states grows too large over a long time horizon. Unlike [1], we present a real-time online motion planning algorithm. We build discrete-time motion primitives and their corresponding continuous-time tubes offline, so that almost all system states of each motion primitive are guaranteed to stay inside the corresponding tube. We convert probabilistic safety constraints into a set of deterministic constraints called risk contours. During online execution, we verify the safety of the tubes against deterministic risk contours using sum-of-squares (SOS) programming. The provided SOS-based method verifies the safety of the tube in the presence of uncertain obstacles without the need for uncertainty samples and time discretization in real-time. By bounding the probability the system states staying inside the tube and bounding the probability of the tube colliding with obstacles, our approach guarantees bounded probability of system states colliding with obstacles. We demonstrate our approach on several long-term robotics tasks.

Chance-Constrained Trajectory Optimization for High-DOF Robots in Uncertain Environments

Many practical applications of robotics require systems that can operate safely despite uncertainty. In the context of motion planning, two types of uncertainty are particularly important when planning safe robot trajectories. The first is environmental uncertainty -- uncertainty in the locations of nearby obstacles, stemming from sensor noise or (in the case of obstacles' future locations) prediction error. The second class of uncertainty is uncertainty in the robots own state, typically caused by tracking or estimation error. To achieve high levels of safety, it is necessary for robots to consider both of these sources of uncertainty. In this paper, we propose a risk-bounded trajectory optimization algorithm, known as Sequential Convex Optimization with Risk Optimization (SCORA), to solve chance-constrained motion planning problems despite both environmental uncertainty and tracking error. Through experiments in simulation, we demonstrate that SCORA significantly outperforms state-of-the-art risk-aware motion planners both in planning time and in the safety of the resulting trajectories.

Automated Deep Aberration Detection from Chromosome Karyotype Images

Chromosome analysis is essential for diagnosing genetic disorders. For hematologic malignancies, identification of somatic clonal aberrations by karyotype analysis remains the standard of care. However, karyotyping is costly and time-consuming because of the largely manual process and the expertise required in identifying and annotating aberrations. Efforts to automate karyotype analysis to date fell short in aberration detection. Using a training set of ~10k patient specimens and ~50k karyograms from over 5 years from the Fred Hutchinson Cancer Center, we created a labeled set of images representing individual chromosomes. These individual chromosomes were used to train and assess deep learning models for classifying the 24 human chromosomes and identifying chromosomal aberrations. The top-accuracy models utilized the recently introduced Topological Vision Transformers (TopViTs) with 2-level-block-Toeplitz masking, to incorporate structural inductive bias. TopViT outperformed CNN (Inception) models with >99.3% accuracy for chromosome identification, and exhibited accuracies >99% for aberration detection in most aberrations. Notably, we were able to show high-quality performance even in "few shot" learning scenarios. Incorporating the definition of clonality substantially improved both precision and recall (sensitivity). When applied to "zero shot" scenarios, the model captured aberrations without training, with perfect precision at >50% recall. Together these results show that modern deep learning models can approach expert-level performance for chromosome aberration detection. To our knowledge, this is the first study demonstrating the downstream effectiveness of TopViTs. These results open up exciting opportunities for not only expediting patient results but providing a scalable technology for early screening of low-abundance chromosomal lesions.

Multi-Agent Chance-Constrained Stochastic Shortest Path with Application to Risk-Aware Intelligent Intersection

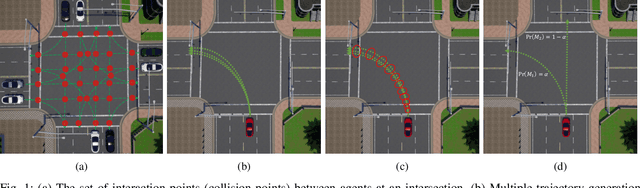
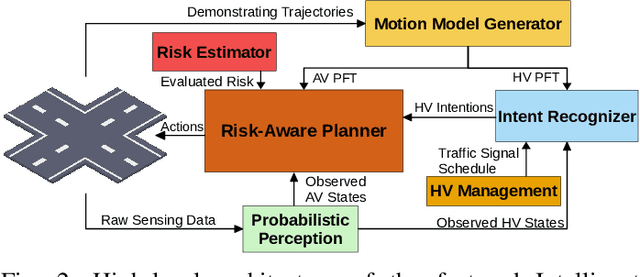
In transportation networks, where traffic lights have traditionally been used for vehicle coordination, intersections act as natural bottlenecks. A formidable challenge for existing automated intersections lies in detecting and reasoning about uncertainty from the operating environment and human-driven vehicles. In this paper, we propose a risk-aware intelligent intersection system for autonomous vehicles (AVs) as well as human-driven vehicles (HVs). We cast the problem as a novel class of Multi-agent Chance-Constrained Stochastic Shortest Path (MCC-SSP) problems and devise an exact Integer Linear Programming (ILP) formulation that is scalable in the number of agents' interaction points (e.g., potential collision points at the intersection). In particular, when the number of agents within an interaction point is small, which is often the case in intersections, the ILP has a polynomial number of variables and constraints. To further improve the running time performance, we show that the collision risk computation can be performed offline. Additionally, a trajectory optimization workflow is provided to generate risk-aware trajectories for any given intersection. The proposed framework is implemented in CARLA simulator and evaluated under a fully autonomous intersection with AVs only as well as in a hybrid setup with a signalized intersection for HVs and an intelligent scheme for AVs. As verified via simulations, the featured approach improves intersection's efficiency by up to $200\%$ while also conforming to the specified tunable risk threshold.

Non-Gaussian Risk Bounded Trajectory Optimization for Stochastic Nonlinear Systems in Uncertain Environments

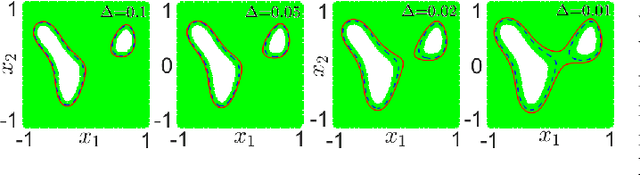
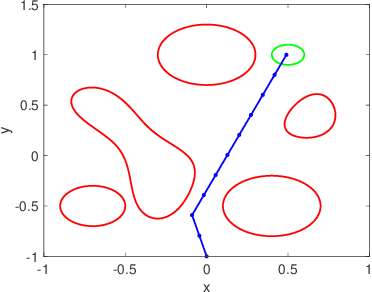
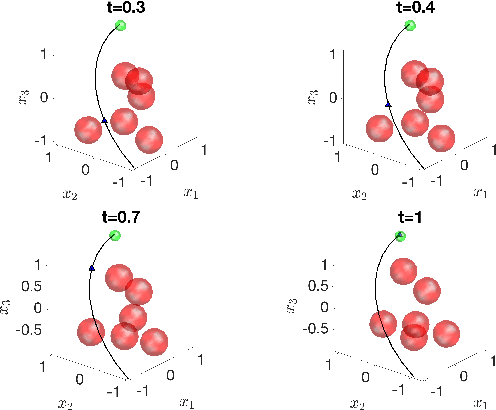
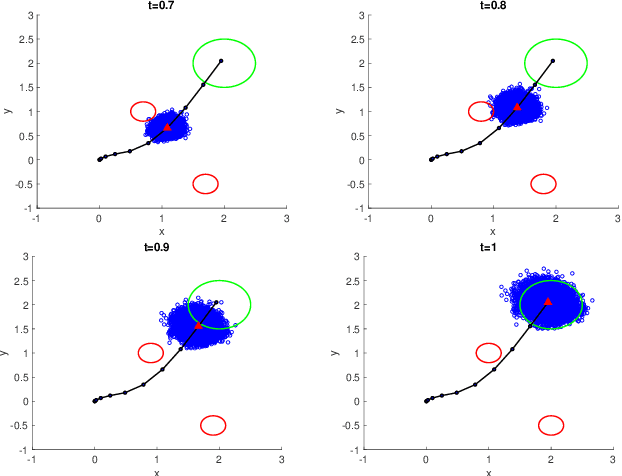
We address the risk bounded trajectory optimization problem of stochastic nonlinear robotic systems. More precisely, we consider the motion planning problem in which the robot has stochastic nonlinear dynamics and uncertain initial locations, and the environment contains multiple dynamic uncertain obstacles with arbitrary probabilistic distributions. The goal is to plan a sequence of control inputs for the robot to navigate to the target while bounding the probability of colliding with obstacles. Existing approaches to address risk bounded trajectory optimization problems are limited to particular classes of models and uncertainties such as Gaussian linear problems. In this paper, we deal with stochastic nonlinear models, nonlinear safety constraints, and arbitrary probabilistic uncertainties, the most general setting ever considered. To address the risk bounded trajectory optimization problem, we first formulate the problem as an optimization problem with stochastic dynamics equations and chance constraints. We then convert probabilistic constraints and stochastic dynamics constraints on random variables into a set of deterministic constraints on the moments of state probability distributions. Finally, we solve the resulting deterministic optimization problem using nonlinear optimization solvers and get a sequence of control inputs. To our best knowledge, it is the first time that the motion planning problem to such a general extent is considered and solved. To illustrate the performance of the proposed method, we provide several robotics examples.

Providing Insights for Open-Response Surveys via End-to-End Context-Aware Clustering

Teachers often conduct surveys in order to collect data from a predefined group of students to gain insights into topics of interest. When analyzing surveys with open-ended textual responses, it is extremely time-consuming, labor-intensive, and difficult to manually process all the responses into an insightful and comprehensive report. In the analysis step, traditionally, the teacher has to read each of the responses and decide on how to group them in order to extract insightful information. Even though it is possible to group the responses only using certain keywords, such an approach would be limited since it not only fails to account for embedded contexts but also cannot detect polysemous words or phrases and semantics that are not expressible in single words. In this work, we present a novel end-to-end context-aware framework that extracts, aggregates, and abbreviates embedded semantic patterns in open-response survey data. Our framework relies on a pre-trained natural language model in order to encode the textual data into semantic vectors. The encoded vectors then get clustered either into an optimally tuned number of groups or into a set of groups with pre-specified titles. In the former case, the clusters are then further analyzed to extract a representative set of keywords or summary sentences that serve as the labels of the clusters. In our framework, for the designated clusters, we finally provide context-aware wordclouds that demonstrate the semantically prominent keywords within each group. Honoring user privacy, we have successfully built the on-device implementation of our framework suitable for real-time analysis on mobile devices and have tested it on a synthetic dataset. Our framework reduces the costs at-scale by automating the process of extracting the most insightful information pieces from survey data.