Non-Gaussian Risk Bounded Trajectory Optimization for Stochastic Nonlinear Systems in Uncertain Environments
Paper and Code
Mar 06, 2022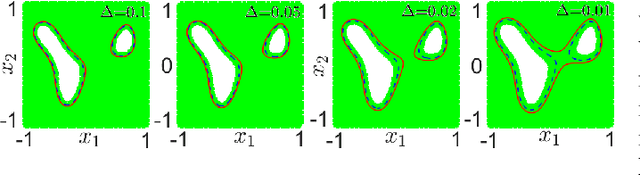
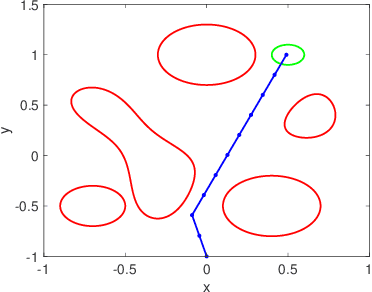
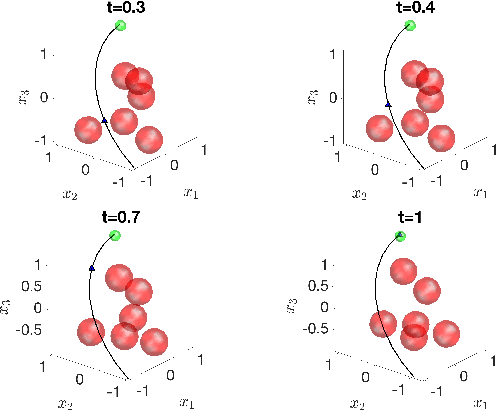
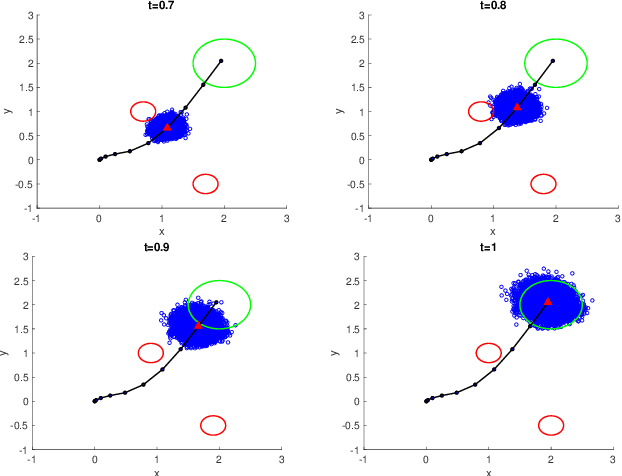
We address the risk bounded trajectory optimization problem of stochastic nonlinear robotic systems. More precisely, we consider the motion planning problem in which the robot has stochastic nonlinear dynamics and uncertain initial locations, and the environment contains multiple dynamic uncertain obstacles with arbitrary probabilistic distributions. The goal is to plan a sequence of control inputs for the robot to navigate to the target while bounding the probability of colliding with obstacles. Existing approaches to address risk bounded trajectory optimization problems are limited to particular classes of models and uncertainties such as Gaussian linear problems. In this paper, we deal with stochastic nonlinear models, nonlinear safety constraints, and arbitrary probabilistic uncertainties, the most general setting ever considered. To address the risk bounded trajectory optimization problem, we first formulate the problem as an optimization problem with stochastic dynamics equations and chance constraints. We then convert probabilistic constraints and stochastic dynamics constraints on random variables into a set of deterministic constraints on the moments of state probability distributions. Finally, we solve the resulting deterministic optimization problem using nonlinear optimization solvers and get a sequence of control inputs. To our best knowledge, it is the first time that the motion planning problem to such a general extent is considered and solved. To illustrate the performance of the proposed method, we provide several robotics examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge