Weiqiao Han
Vector Quantized Feature Fields for Fast 3D Semantic Lifting
Mar 09, 2025
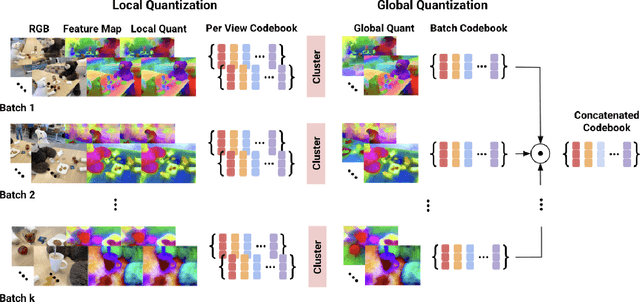


Abstract:We generalize lifting to semantic lifting by incorporating per-view masks that indicate relevant pixels for lifting tasks. These masks are determined by querying corresponding multiscale pixel-aligned feature maps, which are derived from scene representations such as distilled feature fields and feature point clouds. However, storing per-view feature maps rendered from distilled feature fields is impractical, and feature point clouds are expensive to store and query. To enable lightweight on-demand retrieval of pixel-aligned relevance masks, we introduce the Vector-Quantized Feature Field. We demonstrate the effectiveness of the Vector-Quantized Feature Field on complex indoor and outdoor scenes. Semantic lifting, when paired with a Vector-Quantized Feature Field, can unlock a myriad of applications in scene representation and embodied intelligence. Specifically, we showcase how our method enables text-driven localized scene editing and significantly improves the efficiency of embodied question answering.
Convex Risk Bounded Continuous-Time Trajectory Planning and Tube Design in Uncertain Nonconvex Environments
Jun 04, 2023Abstract:In this paper, we address the trajectory planning problem in uncertain nonconvex static and dynamic environments that contain obstacles with probabilistic location, size, and geometry. To address this problem, we provide a risk bounded trajectory planning method that looks for continuous-time trajectories with guaranteed bounded risk over the planning time horizon. Risk is defined as the probability of collision with uncertain obstacles. Existing approaches to address risk bounded trajectory planning problems either are limited to Gaussian uncertainties and convex obstacles or rely on sampling-based methods that need uncertainty samples and time discretization. To address the risk bounded trajectory planning problem, we leverage the notion of risk contours to transform the risk bounded planning problem into a deterministic optimization problem. Risk contours are the set of all points in the uncertain environment with guaranteed bounded risk. The obtained deterministic optimization is, in general, nonlinear and nonconvex time-varying optimization. We provide convex methods based on sum-of-squares optimization to efficiently solve the obtained nonconvex time-varying optimization problem and obtain the continuous-time risk bounded trajectories without time discretization. The provided approach deals with arbitrary (and known) probabilistic uncertainties, nonconvex and nonlinear, static and dynamic obstacles, and is suitable for online trajectory planning problems. In addition, we provide convex methods based on sum-of-squares optimization to build the max-sized tube with respect to its parameterization along the trajectory so that any state inside the tube is guaranteed to have bounded risk.
Non-Gaussian Uncertainty Minimization Based Control of Stochastic Nonlinear Robotic Systems
Mar 02, 2023Abstract:In this paper, we consider the closed-loop control problem of nonlinear robotic systems in the presence of probabilistic uncertainties and disturbances. More precisely, we design a state feedback controller that minimizes deviations of the states of the system from the nominal state trajectories due to uncertainties and disturbances. Existing approaches to address the control problem of probabilistic systems are limited to particular classes of uncertainties and systems such as Gaussian uncertainties and processes and linearized systems. We present an approach that deals with nonlinear dynamics models and arbitrary known probabilistic uncertainties. We formulate the controller design problem as an optimization problem in terms of statistics of the probability distributions including moments and characteristic functions. In particular, in the provided optimization problem, we use moments and characteristic functions to propagate uncertainties throughout the nonlinear motion model of robotic systems. In order to reduce the tracking deviations, we minimize the uncertainty of the probabilistic states around the nominal trajectory by minimizing the trace and the determinant of the covariance matrix of the probabilistic states. To obtain the state feedback gains, we solve deterministic optimization problems in terms of moments, characteristic functions, and state feedback gains using off-the-shelf interior-point optimization solvers. To illustrate the performance of the proposed method, we compare our method with existing probabilistic control methods.
Real-Time Tube-Based Non-Gaussian Risk Bounded Motion Planning for Stochastic Nonlinear Systems in Uncertain Environments via Motion Primitives
Mar 02, 2023Abstract:We consider the motion planning problem for stochastic nonlinear systems in uncertain environments. More precisely, in this problem the robot has stochastic nonlinear dynamics and uncertain initial locations, and the environment contains multiple dynamic uncertain obstacles. Obstacles can be of arbitrary shape, can deform, and can move. All uncertainties do not necessarily have Gaussian distribution. This general setting has been considered and solved in [1]. In addition to the assumptions above, in this paper, we consider long-term tasks, where the planning method in [1] would fail, as the uncertainty of the system states grows too large over a long time horizon. Unlike [1], we present a real-time online motion planning algorithm. We build discrete-time motion primitives and their corresponding continuous-time tubes offline, so that almost all system states of each motion primitive are guaranteed to stay inside the corresponding tube. We convert probabilistic safety constraints into a set of deterministic constraints called risk contours. During online execution, we verify the safety of the tubes against deterministic risk contours using sum-of-squares (SOS) programming. The provided SOS-based method verifies the safety of the tube in the presence of uncertain obstacles without the need for uncertainty samples and time discretization in real-time. By bounding the probability the system states staying inside the tube and bounding the probability of the tube colliding with obstacles, our approach guarantees bounded probability of system states colliding with obstacles. We demonstrate our approach on several long-term robotics tasks.
KEMP: Keyframe-Based Hierarchical End-to-End Deep Model for Long-Term Trajectory Prediction
May 10, 2022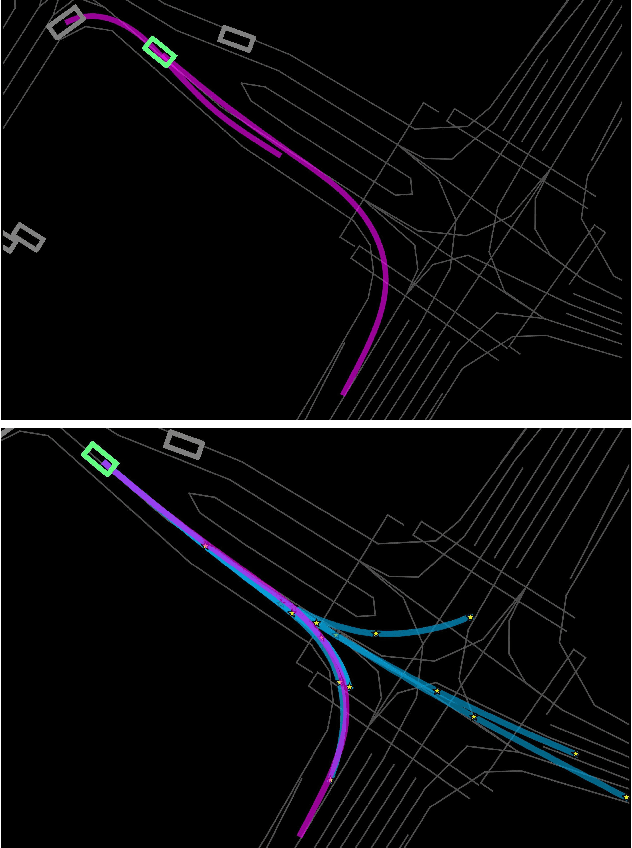
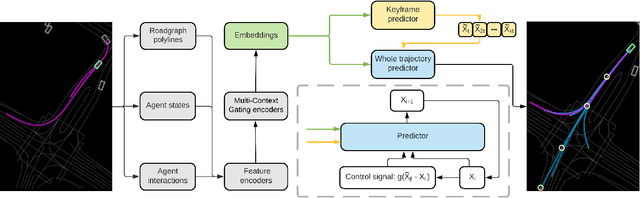
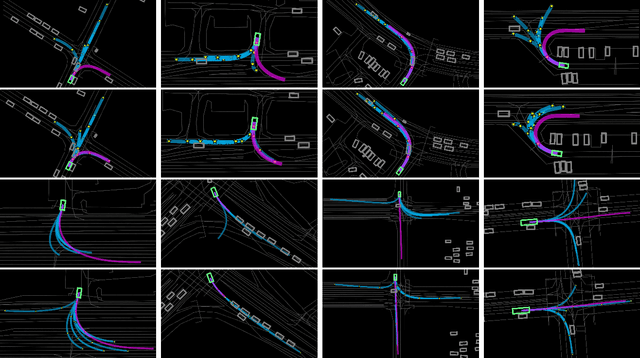
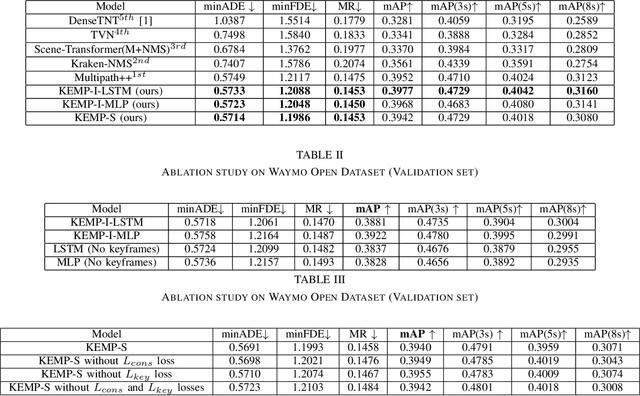
Abstract:Predicting future trajectories of road agents is a critical task for autonomous driving. Recent goal-based trajectory prediction methods, such as DenseTNT and PECNet, have shown good performance on prediction tasks on public datasets. However, they usually require complicated goal-selection algorithms and optimization. In this work, we propose KEMP, a hierarchical end-to-end deep learning framework for trajectory prediction. At the core of our framework is keyframe-based trajectory prediction, where keyframes are representative states that trace out the general direction of the trajectory. KEMP first predicts keyframes conditioned on the road context, and then fills in intermediate states conditioned on the keyframes and the road context. Under our general framework, goal-conditioned methods are special cases in which the number of keyframes equal to one. Unlike goal-conditioned methods, our keyframe predictor is learned automatically and does not require hand-crafted goal-selection algorithms. We evaluate our model on public benchmarks and our model ranked 1st on Waymo Open Motion Dataset Leaderboard (as of September 1, 2021).
Non-Gaussian Risk Bounded Trajectory Optimization for Stochastic Nonlinear Systems in Uncertain Environments
Mar 06, 2022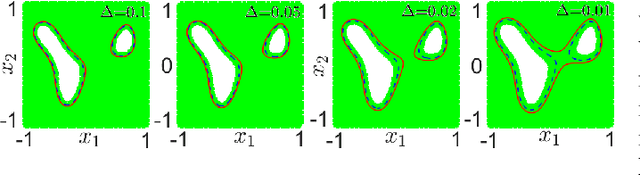
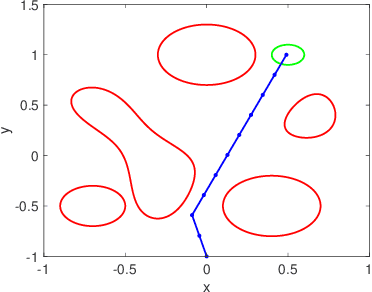
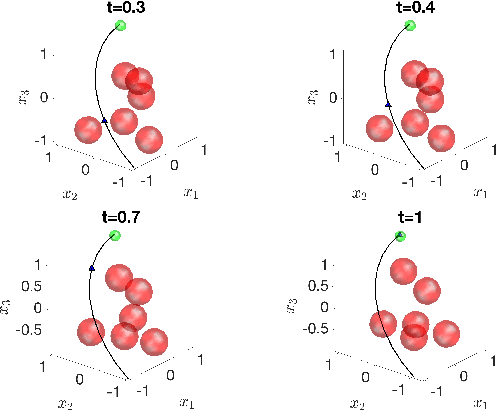
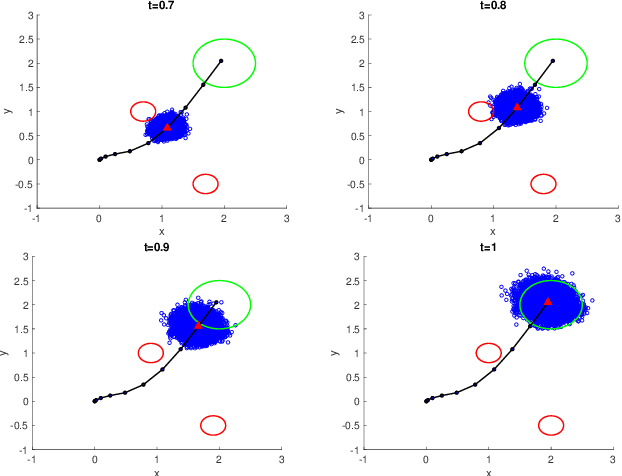
Abstract:We address the risk bounded trajectory optimization problem of stochastic nonlinear robotic systems. More precisely, we consider the motion planning problem in which the robot has stochastic nonlinear dynamics and uncertain initial locations, and the environment contains multiple dynamic uncertain obstacles with arbitrary probabilistic distributions. The goal is to plan a sequence of control inputs for the robot to navigate to the target while bounding the probability of colliding with obstacles. Existing approaches to address risk bounded trajectory optimization problems are limited to particular classes of models and uncertainties such as Gaussian linear problems. In this paper, we deal with stochastic nonlinear models, nonlinear safety constraints, and arbitrary probabilistic uncertainties, the most general setting ever considered. To address the risk bounded trajectory optimization problem, we first formulate the problem as an optimization problem with stochastic dynamics equations and chance constraints. We then convert probabilistic constraints and stochastic dynamics constraints on random variables into a set of deterministic constraints on the moments of state probability distributions. Finally, we solve the resulting deterministic optimization problem using nonlinear optimization solvers and get a sequence of control inputs. To our best knowledge, it is the first time that the motion planning problem to such a general extent is considered and solved. To illustrate the performance of the proposed method, we provide several robotics examples.
Real-Time Risk-Bounded Tube-Based Trajectory Safety Verification
Oct 01, 2021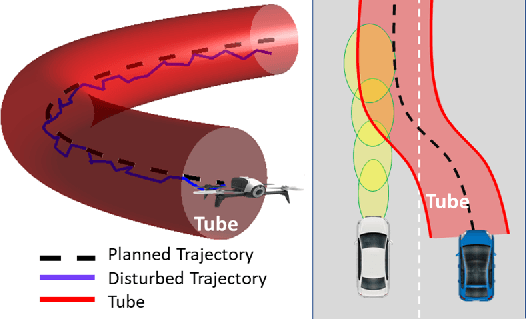


Abstract:In this paper, we address the real-time risk-bounded safety verification problem of continuous-time state trajectories of autonomous systems in the presence of uncertain time-varying nonlinear safety constraints. Risk is defined as the probability of not satisfying the uncertain safety constraints. Existing approaches to address the safety verification problems under uncertainties either are limited to particular classes of uncertainties and safety constraints, e.g., Gaussian uncertainties and linear constraints, or rely on sampling based methods. In this paper, we provide a fast convex algorithm to efficiently evaluate the probabilistic nonlinear safety constraints in the presence of arbitrary probability distributions and long planning horizons in real-time, without the need for uncertainty samples and time discretization. The provided approach verifies the safety of the given state trajectory and its neighborhood (tube) to account for the execution uncertainties and risk. In the provided approach, we first use the moments of the probability distributions of the uncertainties to transform the probabilistic safety constraints into a set of deterministic safety constraints. We then use convex methods based on sum-of-squares polynomials to verify the obtained deterministic safety constraints over the entire planning time horizon without time discretization. To illustrate the performance of the proposed method, we apply the provided method to the safety verification problem of self-driving vehicles and autonomous aerial vehicles.
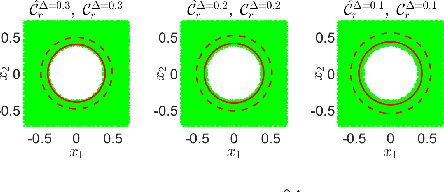
Convex Risk Bounded Continuous-Time Trajectory Planning in Uncertain Nonconvex Environments
Jun 10, 2021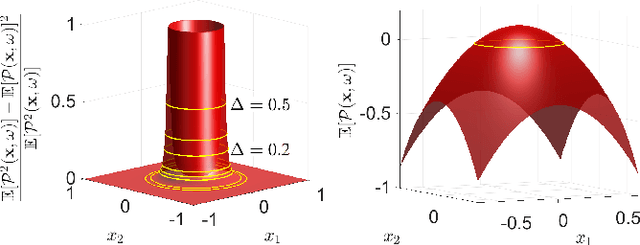
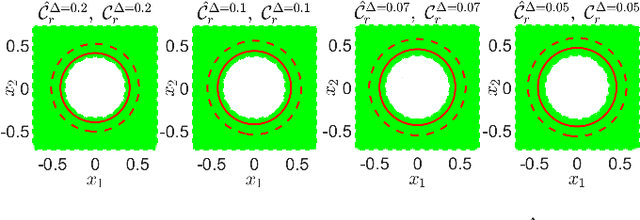
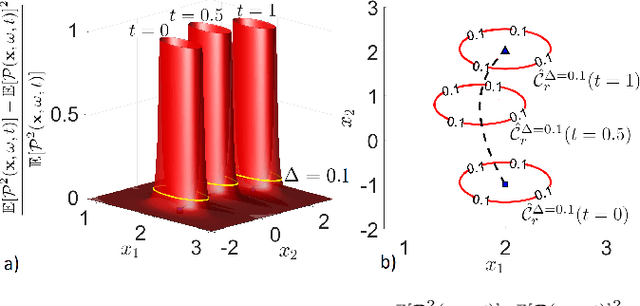
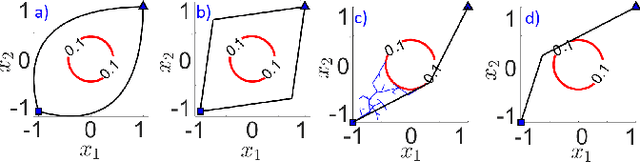
Abstract:In this paper, we address the trajectory planning problem in uncertain nonconvex static and dynamic environments that contain obstacles with probabilistic location, size, and geometry. To address this problem, we provide a risk bounded trajectory planning method that looks for continuous-time trajectories with guaranteed bounded risk over the planning time horizon. Risk is defined as the probability of collision with uncertain obstacles. Existing approaches to address risk bounded trajectory planning problems either are limited to Gaussian uncertainties and convex obstacles or rely on sampling-based methods that need uncertainty samples and time discretization. To address the risk bounded trajectory planning problem, we leverage the notion of risk contours to transform the risk bounded planning problem into a deterministic optimization problem. Risk contours are the set of all points in the uncertain environment with guaranteed bounded risk. The obtained deterministic optimization is, in general, nonlinear and nonconvex time-varying optimization. We provide convex methods based on sum-of-squares optimization to efficiently solve the obtained nonconvex time-varying optimization problem and obtain the continuous-time risk bounded trajectories without time discretization. The provided approach deals with arbitrary probabilistic uncertainties, nonconvex and nonlinear, static and dynamic obstacles, and is suitable for online trajectory planning problems.
Local Trajectory Stabilization for Dexterous Manipulation via Piecewise Affine Approximations
Sep 17, 2019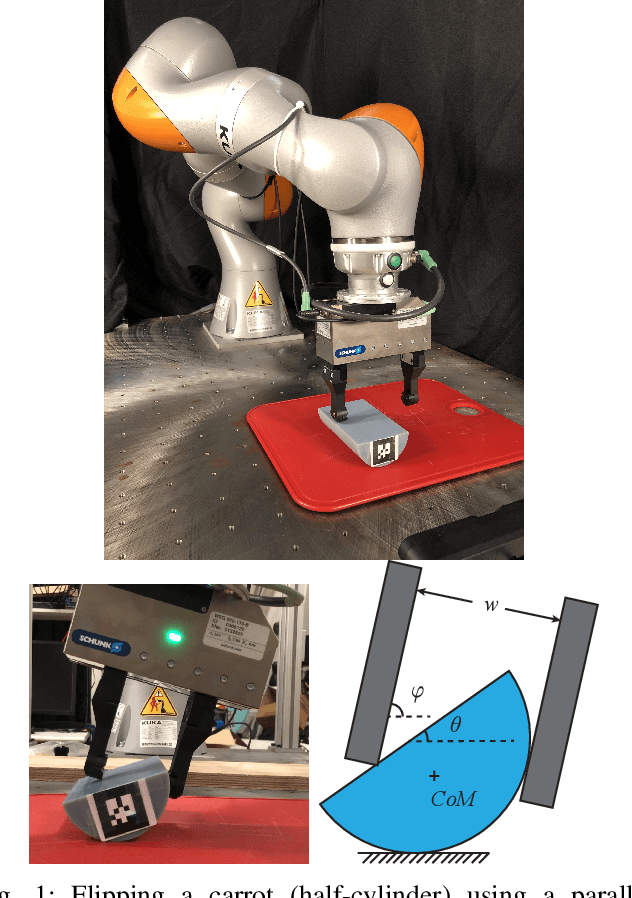

Abstract:We propose a model-based approach to design feedback policies for dexterous robotic manipulation. The manipulation problem is formulated as reaching the target region from an initial state for some non-smooth nonlinear system. First, we use trajectory optimization to find a feasible trajectory. Next, we characterize the local multi-contact dynamics around the trajectory as a piecewise affine system, and build a funnel around the linearization of the nominal trajectory using polytopes. We prove that the feedback controller at the vicinity of the linearization is guaranteed to drive the nonlinear system to the target region. During online execution, we solve linear programs to track the system trajectory. We validate the algorithm on hardware, showing that even under large external disturbances, the controller is able to accomplish the task.
Controller Synthesis for Discrete-time Hybrid Polynomial Systems via Occupation Measures
Sep 16, 2018

Abstract:We present a novel controller synthesis approach for discrete-time hybrid polynomial systems, a class of systems that can model a wide variety of interactions between robots and their environment. The approach is rooted in recently developed techniques that use occupation measures to formulate the controller synthesis problem as an infinite-dimensional linear program. The relaxation of the linear program as a finite-dimensional semidefinite program can be solved to generate a control law. The approach has several advantages including that the formulation is convex, that the formulation and the extracted controllers are simple, and that the computational complexity is polynomial in the state and control input dimensions. We illustrate our approach on some robotics examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge