RELD: Regularization by Latent Diffusion Models for Image Restoration

In recent years, Diffusion Models have become the new state-of-the-art in deep generative modeling, ending the long-time dominance of Generative Adversarial Networks. Inspired by the Regularization by Denoising principle, we introduce an approach that integrates a Latent Diffusion Model, trained for the denoising task, into a variational framework using Half-Quadratic Splitting, exploiting its regularization properties. This approach, under appropriate conditions that can be easily met in various imaging applications, allows for reduced computational cost while achieving high-quality results. The proposed strategy, called Regularization by Latent Denoising (RELD), is then tested on a dataset of natural images, for image denoising, deblurring, and super-resolution tasks. The numerical experiments show that RELD is competitive with other state-of-the-art methods, particularly achieving remarkable results when evaluated using perceptual quality metrics.

TomoSelfDEQ: Self-Supervised Deep Equilibrium Learning for Sparse-Angle CT Reconstruction

Deep learning has emerged as a powerful tool for solving inverse problems in imaging, including computed tomography (CT). However, most approaches require paired training data with ground truth images, which can be difficult to obtain, e.g., in medical applications. We present TomoSelfDEQ, a self-supervised Deep Equilibrium (DEQ) framework for sparse-angle CT reconstruction that trains directly on undersampled measurements. We establish theoretical guarantees showing that, under suitable assumptions, our self-supervised updates match those of fully-supervised training with a loss including the (possibly non-unitary) forward operator like the CT forward map. Numerical experiments on sparse-angle CT data confirm this finding, also demonstrating that TomoSelfDEQ outperforms existing self-supervised methods, achieving state-of-the-art results with as few as 16 projection angles.

Revisiting $Ψ$DONet: microlocally inspired filters for incomplete-data tomographic reconstructions

In this paper, we revisit a supervised learning approach based on unrolling, known as $\Psi$DONet, by providing a deeper microlocal interpretation for its theoretical analysis, and extending its study to the case of sparse-angle tomography. Furthermore, we refine the implementation of the original $\Psi$DONet considering special filters whose structure is specifically inspired by the streak artifact singularities characterizing tomographic reconstructions from incomplete data. This allows to considerably lower the number of (learnable) parameters while preserving (or even slightly improving) the same quality for the reconstructions from limited-angle data and providing a proof-of-concept for the case of sparse-angle tomographic data.

Space-Variant Total Variation boosted by learning techniques in few-view tomographic imaging

This paper focuses on the development of a space-variant regularization model for solving an under-determined linear inverse problem. The case study is a medical image reconstruction from few-view tomographic noisy data. The primary objective of the proposed optimization model is to achieve a good balance between denoising and the preservation of fine details and edges, overcoming the performance of the popular and largely used Total Variation (TV) regularization through the application of appropriate pixel-dependent weights. The proposed strategy leverages the role of gradient approximations for the computation of the space-variant TV weights. For this reason, a convolutional neural network is designed, to approximate both the ground truth image and its gradient using an elastic loss function in its training. Additionally, the paper provides a theoretical analysis of the proposed model, showing the uniqueness of its solution, and illustrates a Chambolle-Pock algorithm tailored to address the specific problem at hand. This comprehensive framework integrates innovative regularization techniques with advanced neural network capabilities, demonstrating promising results in achieving high-quality reconstructions from low-sampled tomographic data.

DeepCEL0 for 2D Single Molecule Localization in Fluorescence Microscopy

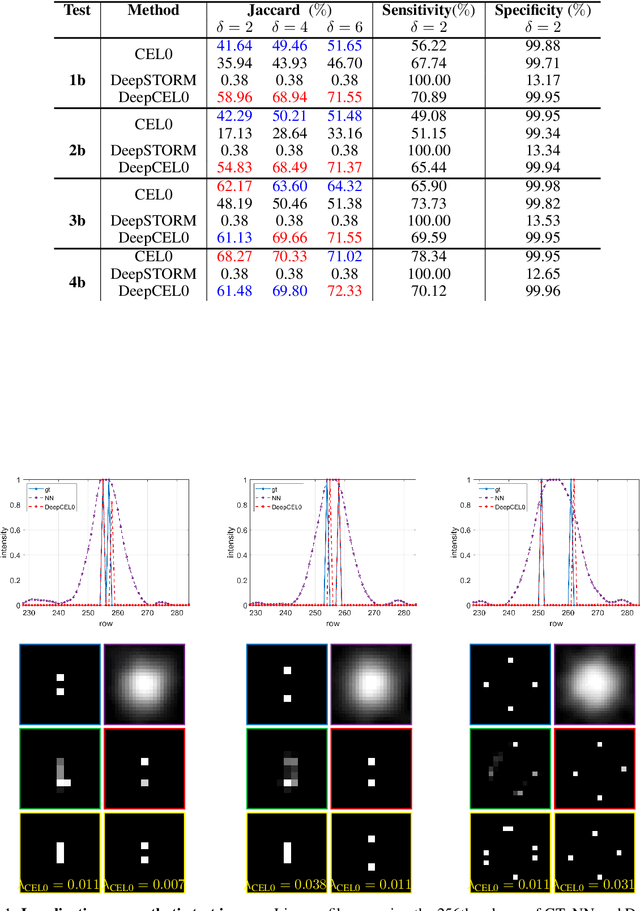
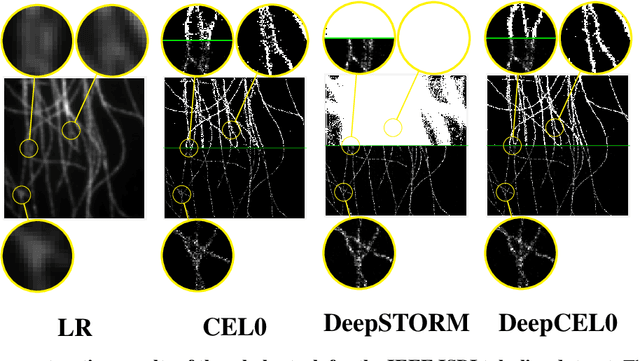
In fluorescence microscopy, Single Molecule Localization Microscopy (SMLM) techniques aim at localizing with high precision high density fluorescent molecules by stochastically activating and imaging small subsets of blinking emitters. Super Resolution (SR) plays an important role in this field since it allows to go beyond the intrinsic light diffraction limit. In this work, we propose a deep learning-based algorithm for precise molecule localization of high density frames acquired by SMLM techniques whose $\ell_{2}$-based loss function is regularized by positivity and $\ell_{0}$-based constraints. The $\ell_{0}$ is relaxed through its Continuous Exact $\ell_{0}$ (CEL0) counterpart. The arising approach, named DeepCEL0, is parameter-free, more flexible, faster and provides more precise molecule localization maps if compared to the other state-of-the-art methods. We validate our approach on both simulated and real fluorescence microscopy data.

Plug-and-Play external and internal priors for image restoration

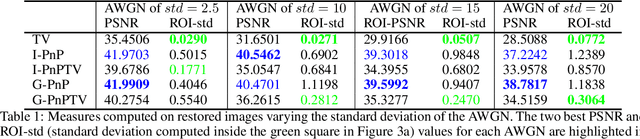
Image restoration problems were traditionally formulated as the minimization of variational models, including data-fidelity and regularization terms, performed by optimization methods with well-established convergence properties. Recently, Plug-and-Play (PnP) methods for image restoration have obtained very good results and popularity by introducing, in iterative proximal algorithms, any off-the-shelf denoiser as priors. Deep Convolutional Neural Network (CNN) denoisers specify external priors (related to an outer training set) which well reflect image statistics; however they fail when dealing with unseen noise variance and image patterns in the given image. Conversely, the so-called internal denoisers induce internal priorsta ilored on the observed data, by forcing specific features on the desired image. We propose a new PnP scheme, based on the Half-Quadratic Splitting proximal algorithm, combining external and internal priors. Moreover, differently from other existing PnP methods, we propose a deep denoiser acting on the image gradient domain. Finally, we prove that a fixed point convergence is guaranteed for the proposed scheme under suitable conditions. In the experimental part, we use CNN denoisers and the Total Variation functional specifying external and internal priors, respectively. We prove the effectiveness of the proposed method in restoring blurred noisy images, both in simulated and real medical settings.