LIP-CAR: contrast agent reduction by a deep learned inverse problem

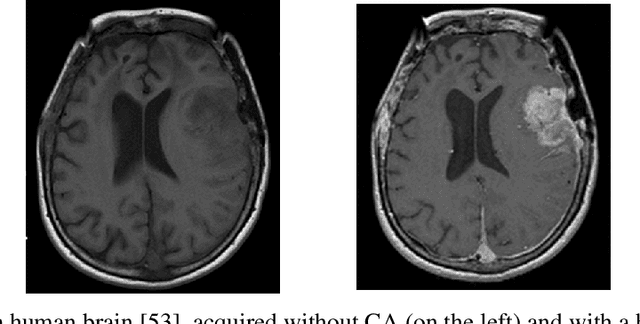
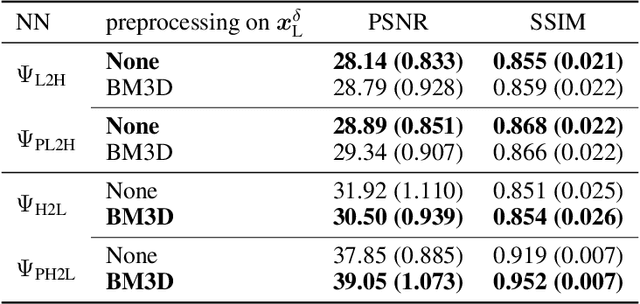
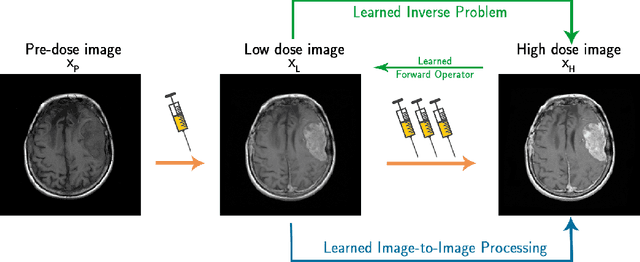
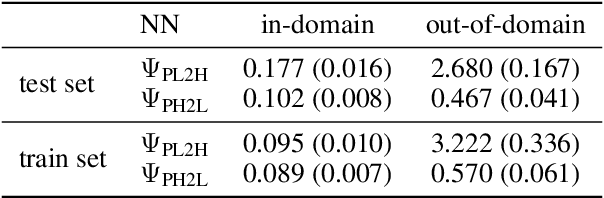
The adoption of contrast agents in medical imaging protocols is crucial for accurate and timely diagnosis. While highly effective and characterized by an excellent safety profile, the use of contrast agents has its limitation, including rare risk of allergic reactions, potential environmental impact and economic burdens on patients and healthcare systems. In this work, we address the contrast agent reduction (CAR) problem, which involves reducing the administered dosage of contrast agent while preserving the visual enhancement. The current literature on the CAR task is based on deep learning techniques within a fully image processing framework. These techniques digitally simulate high-dose images from images acquired with a low dose of contrast agent. We investigate the feasibility of a ``learned inverse problem'' (LIP) approach, as opposed to the end-to-end paradigm in the state-of-the-art literature. Specifically, we learn the image-to-image operator that maps high-dose images to their corresponding low-dose counterparts, and we frame the CAR task as an inverse problem. We then solve this problem through a regularized optimization reformulation. Regularization methods are well-established mathematical techniques that offer robustness and explainability. Our approach combines these rigorous techniques with cutting-edge deep learning tools. Numerical experiments performed on pre-clinical medical images confirm the effectiveness of this strategy, showing improved stability and accuracy in the simulated high-dose images.

Space-Variant Total Variation boosted by learning techniques in few-view tomographic imaging

This paper focuses on the development of a space-variant regularization model for solving an under-determined linear inverse problem. The case study is a medical image reconstruction from few-view tomographic noisy data. The primary objective of the proposed optimization model is to achieve a good balance between denoising and the preservation of fine details and edges, overcoming the performance of the popular and largely used Total Variation (TV) regularization through the application of appropriate pixel-dependent weights. The proposed strategy leverages the role of gradient approximations for the computation of the space-variant TV weights. For this reason, a convolutional neural network is designed, to approximate both the ground truth image and its gradient using an elastic loss function in its training. Additionally, the paper provides a theoretical analysis of the proposed model, showing the uniqueness of its solution, and illustrates a Chambolle-Pock algorithm tailored to address the specific problem at hand. This comprehensive framework integrates innovative regularization techniques with advanced neural network capabilities, demonstrating promising results in achieving high-quality reconstructions from low-sampled tomographic data.

Ambiguity in solving imaging inverse problems with deep learning based operators

In recent years, large convolutional neural networks have been widely used as tools for image deblurring, because of their ability in restoring images very precisely. It is well known that image deblurring is mathematically modeled as an ill-posed inverse problem and its solution is difficult to approximate when noise affects the data. Really, one limitation of neural networks for deblurring is their sensitivity to noise and other perturbations, which can lead to instability and produce poor reconstructions. In addition, networks do not necessarily take into account the numerical formulation of the underlying imaging problem, when trained end-to-end. In this paper, we propose some strategies to improve stability without losing to much accuracy to deblur images with deep-learning based methods. First, we suggest a very small neural architecture, which reduces the execution time for training, satisfying a green AI need, and does not extremely amplify noise in the computed image. Second, we introduce a unified framework where a pre-processing step balances the lack of stability of the following, neural network-based, step. Two different pre-processors are presented: the former implements a strong parameter-free denoiser, and the latter is a variational model-based regularized formulation of the latent imaging problem. This framework is also formally characterized by mathematical analysis. Numerical experiments are performed to verify the accuracy and stability of the proposed approaches for image deblurring when unknown or not-quantified noise is present; the results confirm that they improve the network stability with respect to noise. In particular, the model-based framework represents the most reliable trade-off between visual precision and robustness.

To be or not to be stable, that is the question: understanding neural networks for inverse problems

The solution of linear inverse problems arising, for example, in signal and image processing is a challenging problem, since the ill-conditioning amplifies the noise on the data. Recently introduced deep-learning based algorithms overwhelm the more traditional model-based approaches but they typically suffer from instability with respect to data perturbation. In this paper, we theoretically analyse the trade-off between neural networks stability and accuracy in the solution of linear inverse problems. Moreover, we propose different supervised and unsupervised solutions, to increase network stability by maintaining good accuracy, by inheriting, in the network training, regularization from a model-based iterative scheme. Extensive numerical experiments on image deblurring confirm the theoretical results and the effectiveness of the proposed networks in solving inverse problems with stability with respect to noise.

Dissecting FLOPs along input dimensions for GreenAI cost estimations

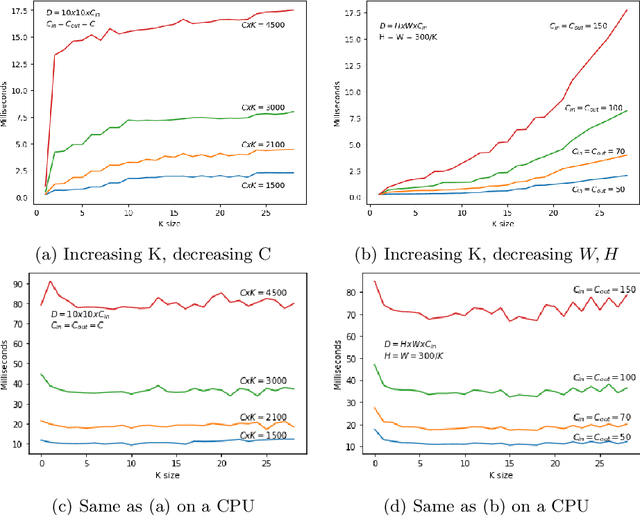
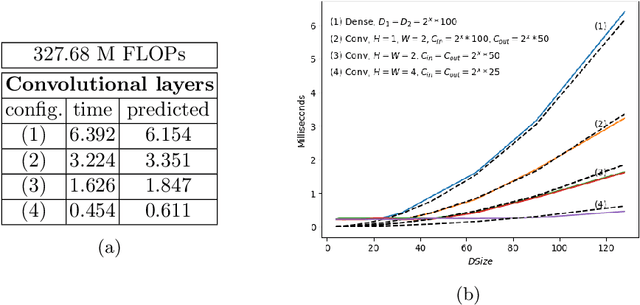
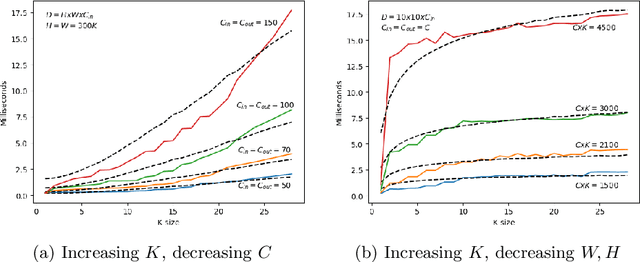
The term GreenAI refers to a novel approach to Deep Learning, that is more aware of the ecological impact and the computational efficiency of its methods. The promoters of GreenAI suggested the use of Floating Point Operations (FLOPs) as a measure of the computational cost of Neural Networks; however, that measure does not correlate well with the energy consumption of hardware equipped with massively parallel processing units like GPUs or TPUs. In this article, we propose a simple refinement of the formula used to compute floating point operations for convolutional layers, called {\alpha}-FLOPs, explaining and correcting the traditional discrepancy with respect to different layers, and closer to reality. The notion of {\alpha}-FLOPs relies on the crucial insight that, in case of inputs with multiple dimensions, there is no reason to believe that the speedup offered by parallelism will be uniform along all different axes.