Ambiguity in solving imaging inverse problems with deep learning based operators

In recent years, large convolutional neural networks have been widely used as tools for image deblurring, because of their ability in restoring images very precisely. It is well known that image deblurring is mathematically modeled as an ill-posed inverse problem and its solution is difficult to approximate when noise affects the data. Really, one limitation of neural networks for deblurring is their sensitivity to noise and other perturbations, which can lead to instability and produce poor reconstructions. In addition, networks do not necessarily take into account the numerical formulation of the underlying imaging problem, when trained end-to-end. In this paper, we propose some strategies to improve stability without losing to much accuracy to deblur images with deep-learning based methods. First, we suggest a very small neural architecture, which reduces the execution time for training, satisfying a green AI need, and does not extremely amplify noise in the computed image. Second, we introduce a unified framework where a pre-processing step balances the lack of stability of the following, neural network-based, step. Two different pre-processors are presented: the former implements a strong parameter-free denoiser, and the latter is a variational model-based regularized formulation of the latent imaging problem. This framework is also formally characterized by mathematical analysis. Numerical experiments are performed to verify the accuracy and stability of the proposed approaches for image deblurring when unknown or not-quantified noise is present; the results confirm that they improve the network stability with respect to noise. In particular, the model-based framework represents the most reliable trade-off between visual precision and robustness.

To be or not to be stable, that is the question: understanding neural networks for inverse problems

The solution of linear inverse problems arising, for example, in signal and image processing is a challenging problem, since the ill-conditioning amplifies the noise on the data. Recently introduced deep-learning based algorithms overwhelm the more traditional model-based approaches but they typically suffer from instability with respect to data perturbation. In this paper, we theoretically analyse the trade-off between neural networks stability and accuracy in the solution of linear inverse problems. Moreover, we propose different supervised and unsupervised solutions, to increase network stability by maintaining good accuracy, by inheriting, in the network training, regularization from a model-based iterative scheme. Extensive numerical experiments on image deblurring confirm the theoretical results and the effectiveness of the proposed networks in solving inverse problems with stability with respect to noise.

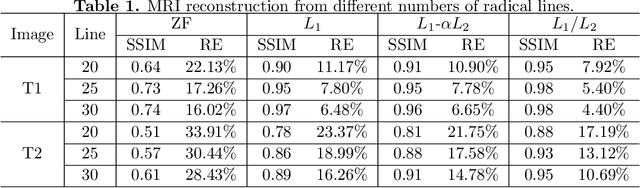
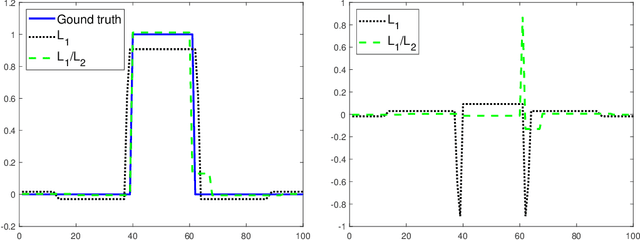
Minimizing L1 over L2 norms on the gradient

In this paper, we study the L1/L2 minimization on the gradient for imaging applications. Several recent works have demonstrated that L1/L2 is better than the L1 norm when approximating the L0 norm to promote sparsity. Consequently, we postulate that applying L1/L2 on the gradient is better than the classic total variation (the L1 norm on the gradient) to enforce the sparsity of the image gradient. To verify our hypothesis, we consider a constrained formulation to reveal empirical evidence on the superiority of L1/L2 over L1 when recovering piecewise constant signals from low-frequency measurements. Numerically, we design a specific splitting scheme, under which we can prove the subsequential convergence for the alternating direction method of multipliers (ADMM). Experimentally, we demonstrate visible improvements of L1/L2 over L1 and other nonconvex regularizations for image recovery from low-frequency measurements and two medical applications of MRI and CT reconstruction. All the numerical results show the efficiency of our proposed approach.

Limited-angle CT reconstruction via the L1/L2 minimization

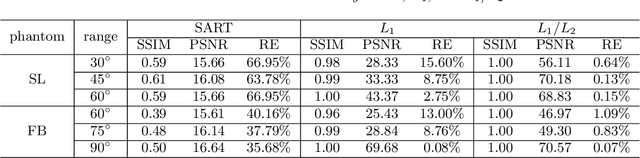
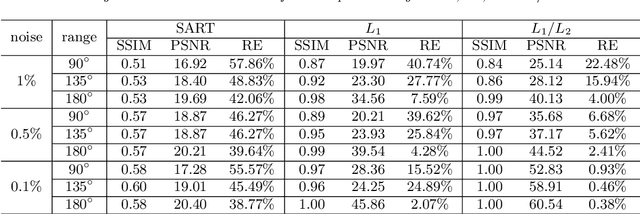
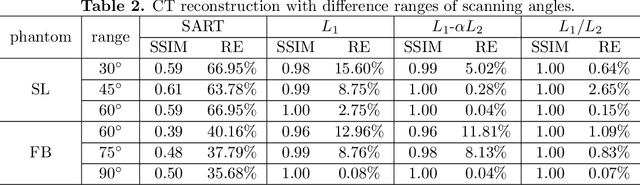
In this paper, we consider minimizing the L1/L2 term on the gradient for a limit-angle scanning problem in computed tomography (CT) reconstruction. We design a splitting framework for both constrained and unconstrained optimization models. In addition, we can incorporate a box constraint that is reasonable for imaging applications. Numerical schemes are based on the alternating direction method of multipliers (ADMM), and we provide the convergence analysis of all the proposed algorithms (constrained/unconstrained and with/without the box constraint). Experimental results demonstrate the efficiency of our proposed approaches, showing significant improvements over the state-of-the-art methods in the limit-angle CT reconstruction. Specifically worth noticing is an exact recovery of the Shepp-Logan phantom from noiseless projection data with 30 scanning angle.

LAP: a Linearize and Project Method for Solving Inverse Problems with Coupled Variables

Many inverse problems involve two or more sets of variables that represent different physical quantities but are tightly coupled with each other. For example, image super-resolution requires joint estimation of the image and motion parameters from noisy measurements. Exploiting this structure is key for efficiently solving these large-scale optimization problems, which are often ill-conditioned. In this paper, we present a new method called Linearize And Project (LAP) that offers a flexible framework for solving inverse problems with coupled variables. LAP is most promising for cases when the subproblem corresponding to one of the variables is considerably easier to solve than the other. LAP is based on a Gauss-Newton method, and thus after linearizing the residual, it eliminates one block of variables through projection. Due to the linearization, this block can be chosen freely. Further, LAP supports direct, iterative, and hybrid regularization as well as constraints. Therefore LAP is attractive, e.g., for ill-posed imaging problems. These traits differentiate LAP from common alternatives for this type of problem such as variable projection (VarPro) and block coordinate descent (BCD). Our numerical experiments compare the performance of LAP to BCD and VarPro using three coupled problems whose forward operators are linear with respect to one block and nonlinear for the other set of variables.