Minimizing L1 over L2 norms on the gradient
Paper and Code
Jan 04, 2021
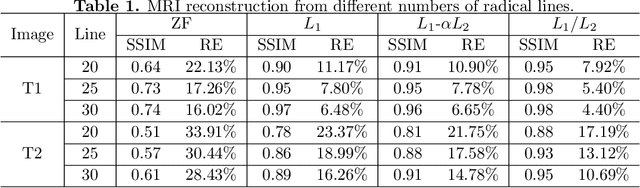
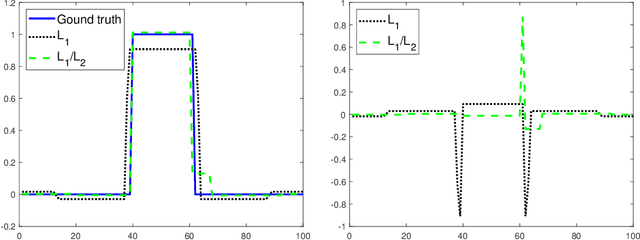
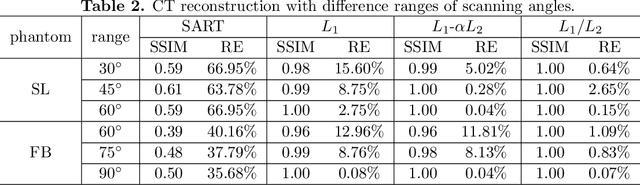
In this paper, we study the L1/L2 minimization on the gradient for imaging applications. Several recent works have demonstrated that L1/L2 is better than the L1 norm when approximating the L0 norm to promote sparsity. Consequently, we postulate that applying L1/L2 on the gradient is better than the classic total variation (the L1 norm on the gradient) to enforce the sparsity of the image gradient. To verify our hypothesis, we consider a constrained formulation to reveal empirical evidence on the superiority of L1/L2 over L1 when recovering piecewise constant signals from low-frequency measurements. Numerically, we design a specific splitting scheme, under which we can prove the subsequential convergence for the alternating direction method of multipliers (ADMM). Experimentally, we demonstrate visible improvements of L1/L2 over L1 and other nonconvex regularizations for image recovery from low-frequency measurements and two medical applications of MRI and CT reconstruction. All the numerical results show the efficiency of our proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge