LIP-CAR: contrast agent reduction by a deep learned inverse problem

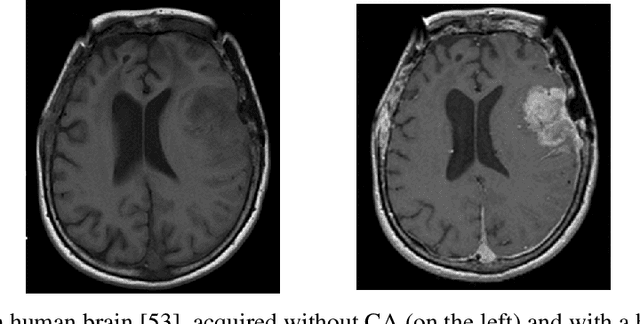
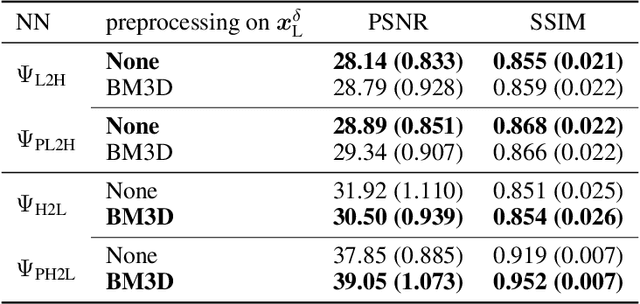
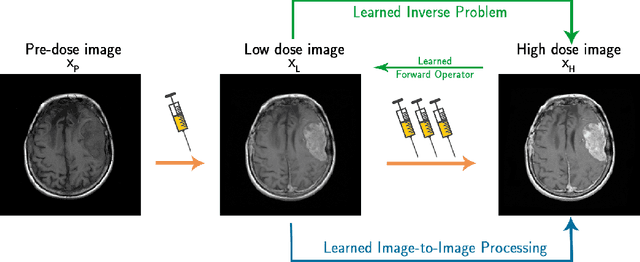
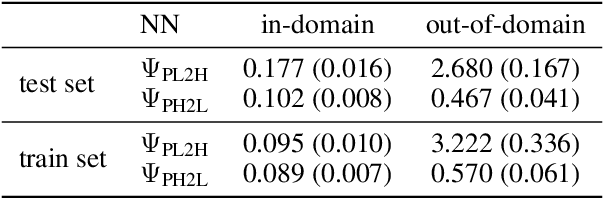
The adoption of contrast agents in medical imaging protocols is crucial for accurate and timely diagnosis. While highly effective and characterized by an excellent safety profile, the use of contrast agents has its limitation, including rare risk of allergic reactions, potential environmental impact and economic burdens on patients and healthcare systems. In this work, we address the contrast agent reduction (CAR) problem, which involves reducing the administered dosage of contrast agent while preserving the visual enhancement. The current literature on the CAR task is based on deep learning techniques within a fully image processing framework. These techniques digitally simulate high-dose images from images acquired with a low dose of contrast agent. We investigate the feasibility of a ``learned inverse problem'' (LIP) approach, as opposed to the end-to-end paradigm in the state-of-the-art literature. Specifically, we learn the image-to-image operator that maps high-dose images to their corresponding low-dose counterparts, and we frame the CAR task as an inverse problem. We then solve this problem through a regularized optimization reformulation. Regularization methods are well-established mathematical techniques that offer robustness and explainability. Our approach combines these rigorous techniques with cutting-edge deep learning tools. Numerical experiments performed on pre-clinical medical images confirm the effectiveness of this strategy, showing improved stability and accuracy in the simulated high-dose images.

Improved impedance inversion by deep learning and iterated graph Laplacian

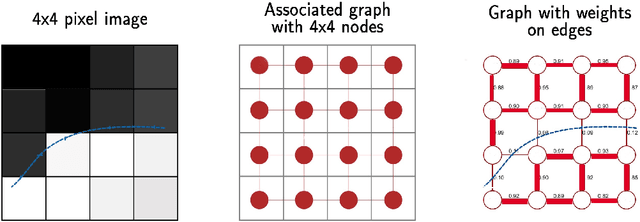
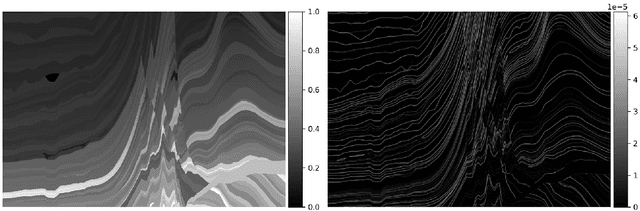
Deep learning techniques have shown significant potential in many applications through recent years. The achieved results often outperform traditional techniques. However, the quality of a neural network highly depends on the used training data. Noisy, insufficient, or biased training data leads to suboptimal results. We present a hybrid method that combines deep learning with iterated graph Laplacian and show its application in acoustic impedance inversion which is a routine procedure in seismic explorations. A neural network is used to obtain a first approximation of the underlying acoustic impedance and construct a graph Laplacian matrix from this approximation. Afterwards, we use a Tikhonov-like variational method to solve the impedance inversion problem where the regularizer is based on the constructed graph Laplacian. The obtained solution can be shown to be more accurate and stable with respect to noise than the initial guess obtained by the neural network. This process can be iterated several times, each time constructing a new graph Laplacian matrix from the most recent reconstruction. The method converges after only a few iterations returning a much more accurate reconstruction. We demonstrate the potential of our method on two different datasets and under various levels of noise. We use two different neural networks that have been introduced in previous works. The experiments show that our approach improves the reconstruction quality in the presence of noise.