Improved impedance inversion by deep learning and iterated graph Laplacian
Paper and Code
Apr 25, 2024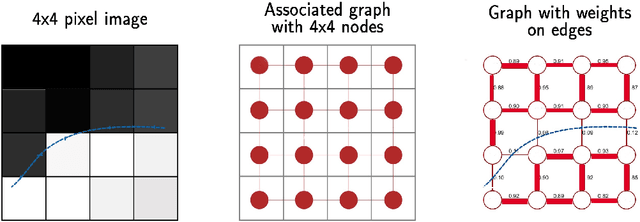
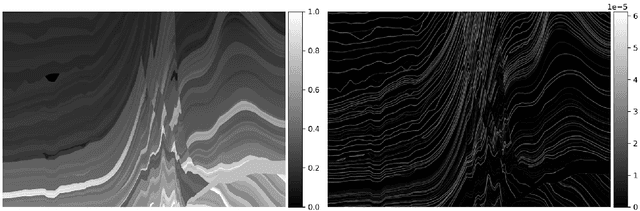
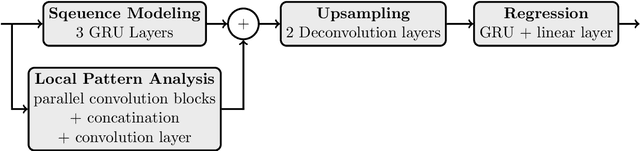
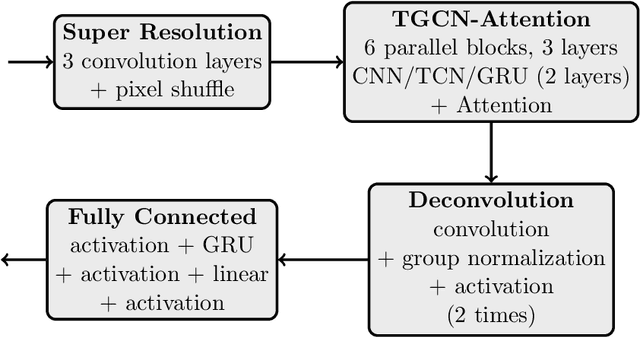
Deep learning techniques have shown significant potential in many applications through recent years. The achieved results often outperform traditional techniques. However, the quality of a neural network highly depends on the used training data. Noisy, insufficient, or biased training data leads to suboptimal results. We present a hybrid method that combines deep learning with iterated graph Laplacian and show its application in acoustic impedance inversion which is a routine procedure in seismic explorations. A neural network is used to obtain a first approximation of the underlying acoustic impedance and construct a graph Laplacian matrix from this approximation. Afterwards, we use a Tikhonov-like variational method to solve the impedance inversion problem where the regularizer is based on the constructed graph Laplacian. The obtained solution can be shown to be more accurate and stable with respect to noise than the initial guess obtained by the neural network. This process can be iterated several times, each time constructing a new graph Laplacian matrix from the most recent reconstruction. The method converges after only a few iterations returning a much more accurate reconstruction. We demonstrate the potential of our method on two different datasets and under various levels of noise. We use two different neural networks that have been introduced in previous works. The experiments show that our approach improves the reconstruction quality in the presence of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge