Learning a Gaussian Mixture for Sparsity Regularization in Inverse Problems

In inverse problems, it is widely recognized that the incorporation of a sparsity prior yields a regularization effect on the solution. This approach is grounded on the a priori assumption that the unknown can be appropriately represented in a basis with a limited number of significant components, while most coefficients are close to zero. This occurrence is frequently observed in real-world scenarios, such as with piecewise smooth signals. In this study, we propose a probabilistic sparsity prior formulated as a mixture of degenerate Gaussians, capable of modeling sparsity with respect to a generic basis. Under this premise, we design a neural network that can be interpreted as the Bayes estimator for linear inverse problems. Additionally, we put forth both a supervised and an unsupervised training strategy to estimate the parameters of this network. To evaluate the effectiveness of our approach, we conduct a numerical comparison with commonly employed sparsity-promoting regularization techniques, namely LASSO, group LASSO, iterative hard thresholding, and sparse coding/dictionary learning. Notably, our reconstructions consistently exhibit lower mean square error values across all $1$D datasets utilized for the comparisons, even in cases where the datasets significantly deviate from a Gaussian mixture model.

Manifold Learning by Mixture Models of VAEs for Inverse Problems

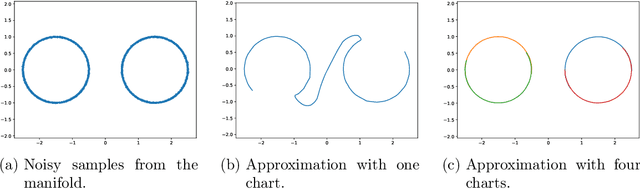
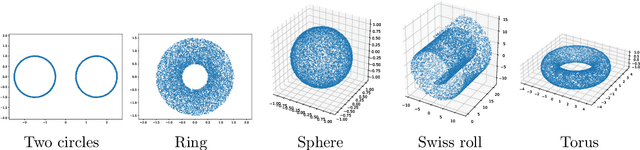
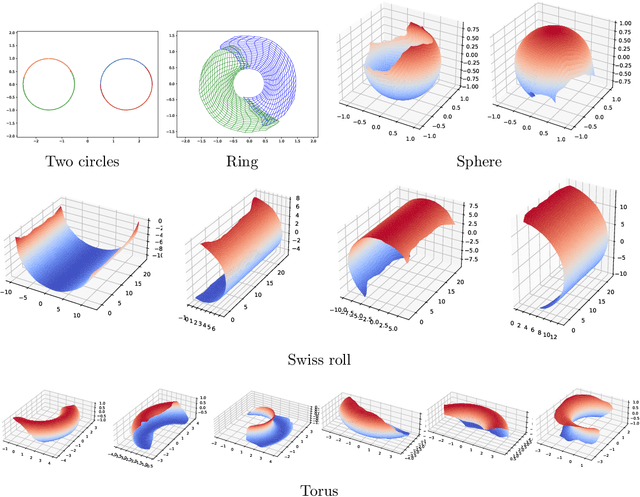
Representing a manifold of very high-dimensional data with generative models has been shown to be computationally efficient in practice. However, this requires that the data manifold admits a global parameterization. In order to represent manifolds of arbitrary topology, we propose to learn a mixture model of variational autoencoders. Here, every encoder-decoder pair represents one chart of a manifold. We propose a loss function for maximum likelihood estimation of the model weights and choose an architecture that provides us the analytical expression of the charts and of their inverses. Once the manifold is learned, we use it for solving inverse problems by minimizing a data fidelity term restricted to the learned manifold. To solve the arising minimization problem we propose a Riemannian gradient descent algorithm on the learned manifold. We demonstrate the performance of our method for low-dimensional toy examples as well as for deblurring and electrical impedance tomography on certain image manifolds.

Continuous Generative Neural Networks

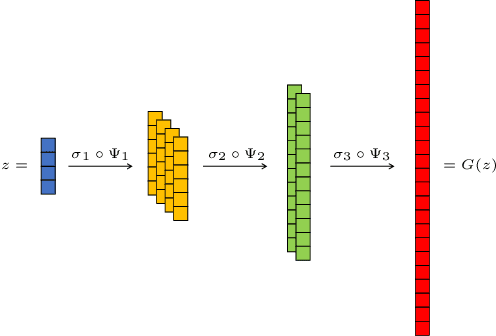
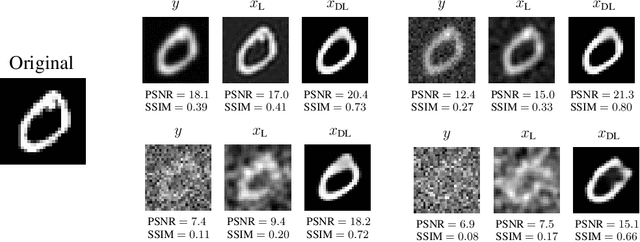
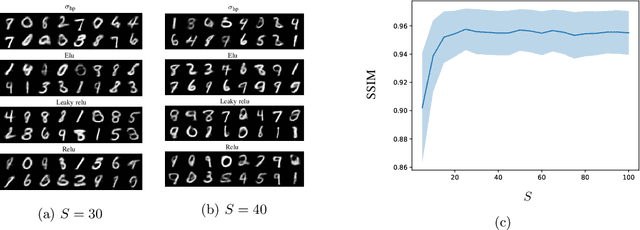
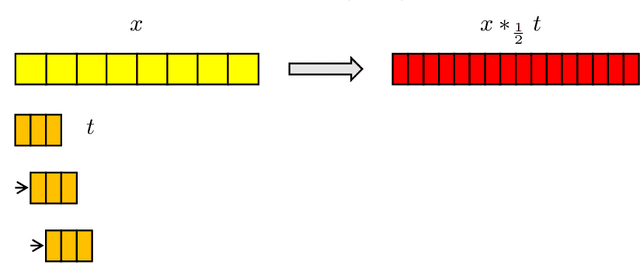
In this work, we present and study Continuous Generative Neural Networks (CGNNs), namely, generative models in the continuous setting. The architecture is inspired by DCGAN, with one fully connected layer, several convolutional layers and nonlinear activation functions. In the continuous $L^2$ setting, the dimensions of the spaces of each layer are replaced by the scales of a multiresolution analysis of a compactly supported wavelet. We present conditions on the convolutional filters and on the nonlinearity that guarantee that a CGNN is injective. This theory finds applications to inverse problems, and allows for deriving Lipschitz stability estimates for (possibly nonlinear) infinite-dimensional inverse problems with unknowns belonging to the manifold generated by a CGNN. Several numerical simulations, including image deblurring, illustrate and validate this approach.