Geometry of contact: contact planning for multi-legged robots via spin models duality

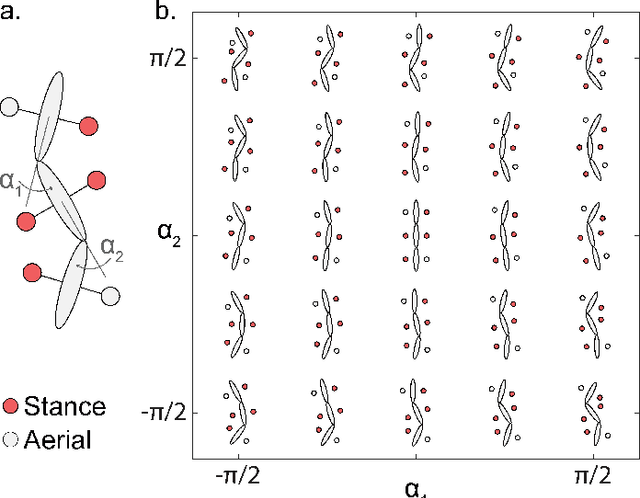
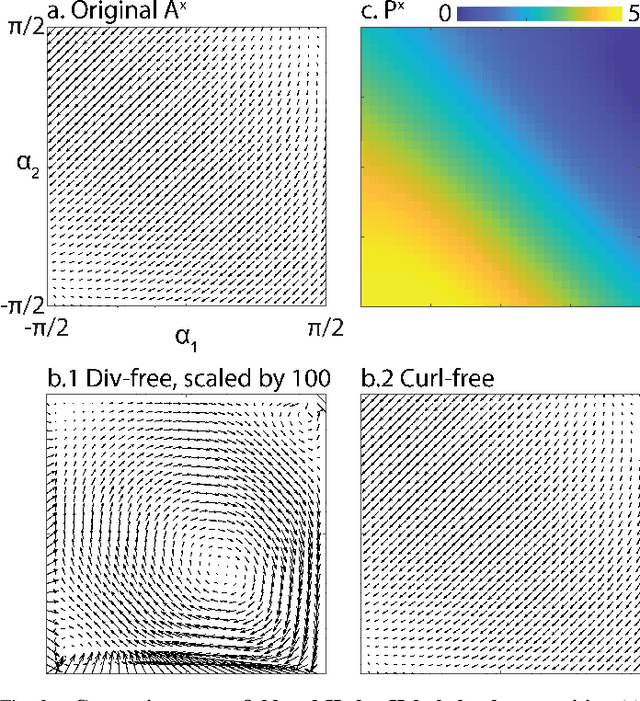
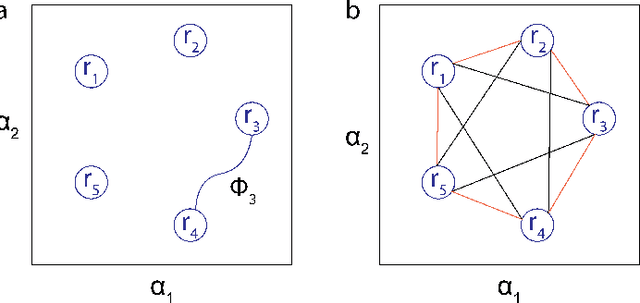
Contact planning is crucial in locomoting systems.Specifically, appropriate contact planning can enable versatile behaviors (e.g., sidewinding in limbless locomotors) and facilitate speed-dependent gait transitions (e.g., walk-trot-gallop in quadrupedal locomotors). The challenges of contact planning include determining not only the sequence by which contact is made and broken between the locomotor and the environments, but also the sequence of internal shape changes (e.g., body bending and limb shoulder joint oscillation). Most state-of-art contact planning algorithms focused on conventional robots (e.g.biped and quadruped) and conventional tasks (e.g. forward locomotion), and there is a lack of study on general contact planning in multi-legged robots. In this paper, we show that using geometric mechanics framework, we can obtain the global optimal contact sequence given the internal shape changes sequence. Therefore, we simplify the contact planning problem to a graph optimization problem to identify the internal shape changes. Taking advantages of the spatio-temporal symmetry in locomotion, we map the graph optimization problem to special cases of spin models, which allows us to obtain the global optima in polynomial time. We apply our approach to develop new forward and sidewinding behaviors in a hexapod and a 12-legged centipede. We verify our predictions using numerical and robophysical models, and obtain novel and effective locomotion behaviors.

Informative Neural Ensemble Kalman Learning

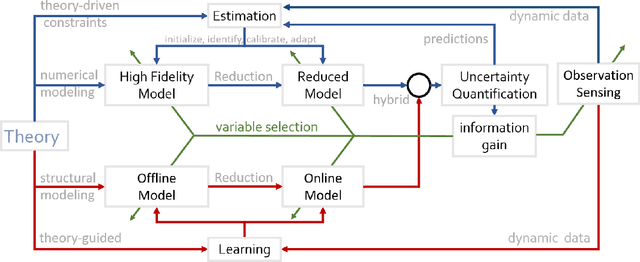
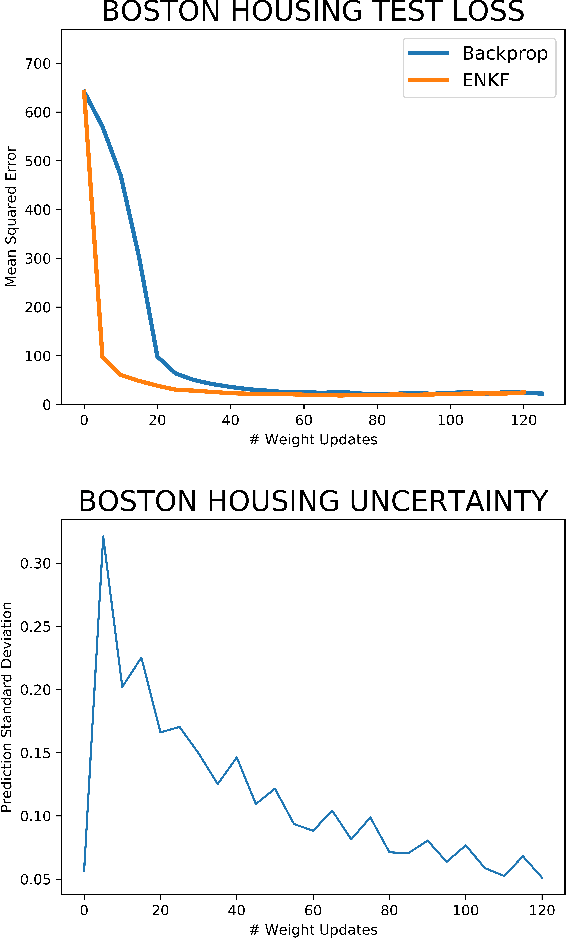
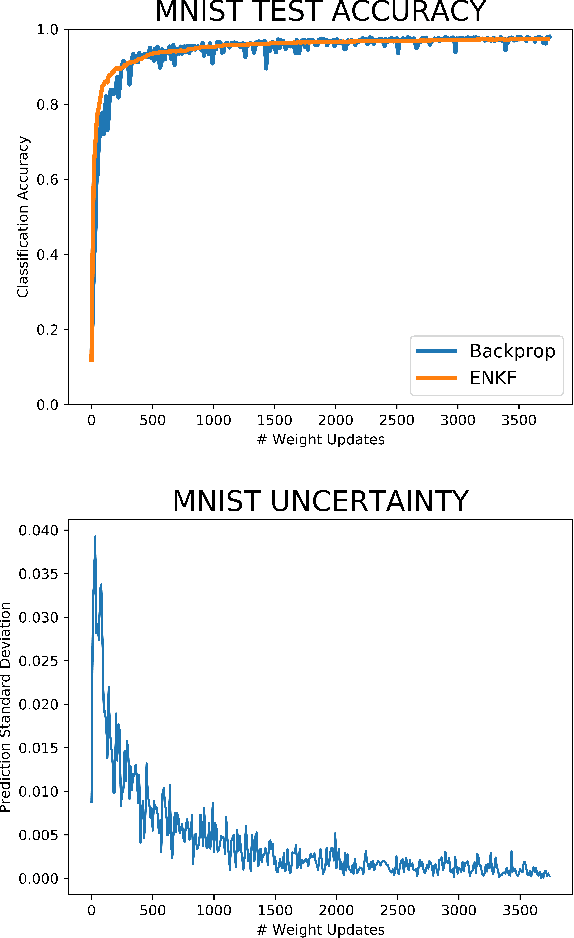
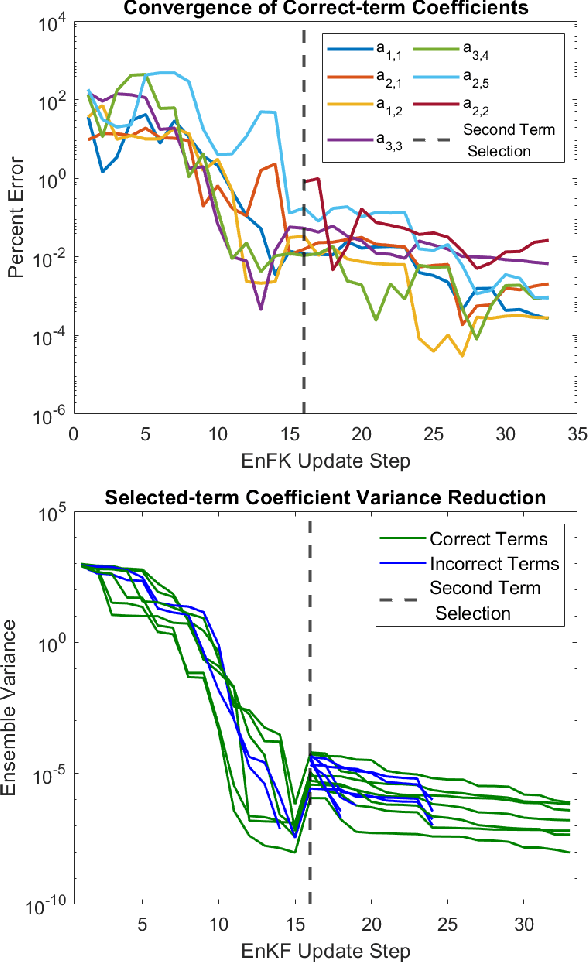
In stochastic systems, informative approaches select key measurement or decision variables that maximize information gain to enhance the efficacy of model-related inferences. Neural Learning also embodies stochastic dynamics, but informative Learning is less developed. Here, we propose Informative Ensemble Kalman Learning, which replaces backpropagation with an adaptive Ensemble Kalman Filter to quantify uncertainty and enables maximizing information gain during Learning. After demonstrating Ensemble Kalman Learning's competitive performance on standard datasets, we apply the informative approach to neural structure learning. In particular, we show that when trained from the Lorenz-63 system's simulations, the efficaciously learned structure recovers the dynamical equations. To the best of our knowledge, Informative Ensemble Kalman Learning is new. Results suggest that this approach to optimized Learning is promising.