Optimal transport for automatic alignment of untargeted metabolomic data

Untargeted metabolomic profiling through liquid chromatography-mass spectrometry (LC-MS) measures a vast array of metabolites within biospecimens, advancing drug development, disease diagnosis, and risk prediction. However, the low throughput of LC-MS poses a major challenge for biomarker discovery, annotation, and experimental comparison, necessitating the merging of multiple datasets. Current data pooling methods encounter practical limitations due to their vulnerability to data variations and hyperparameter dependence. Here we introduce GromovMatcher, a flexible and user-friendly algorithm that automatically combines LC-MS datasets using optimal transport. By capitalizing on feature intensity correlation structures, GromovMatcher delivers superior alignment accuracy and robustness compared to existing approaches. This algorithm scales to thousands of features requiring minimal hyperparameter tuning. Applying our method to experimental patient studies of liver and pancreatic cancer, we discover shared metabolic features related to patient alcohol intake, demonstrating how GromovMatcher facilitates the search for biomarkers associated with lifestyle risk factors linked to several cancer types.

Safe Feature Elimination for the LASSO and Sparse Supervised Learning Problems

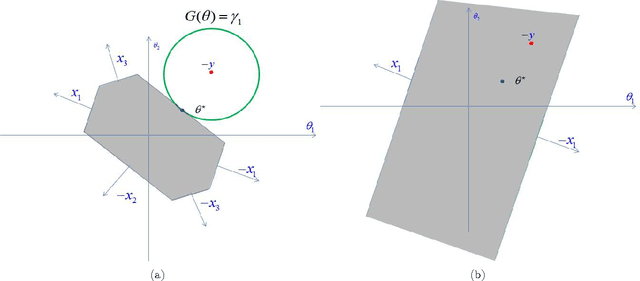
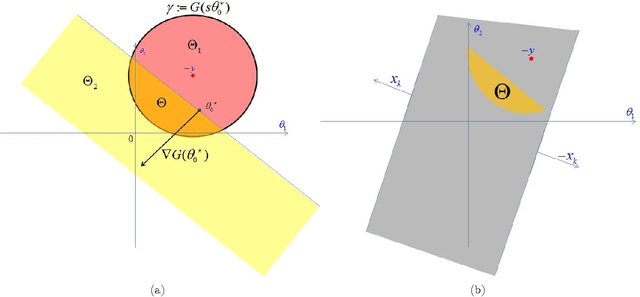
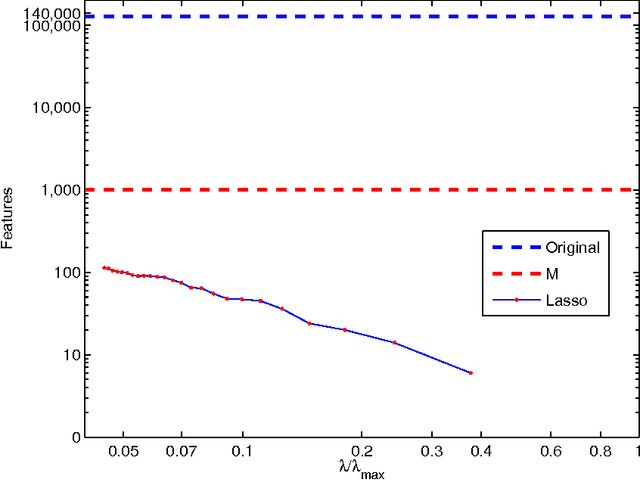
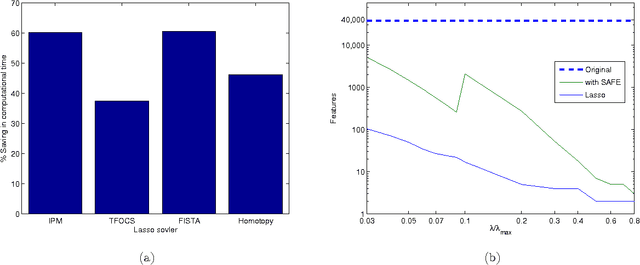
We describe a fast method to eliminate features (variables) in l1 -penalized least-square regression (or LASSO) problems. The elimination of features leads to a potentially substantial reduction in running time, specially for large values of the penalty parameter. Our method is not heuristic: it only eliminates features that are guaranteed to be absent after solving the LASSO problem. The feature elimination step is easy to parallelize and can test each feature for elimination independently. Moreover, the computational effort of our method is negligible compared to that of solving the LASSO problem - roughly it is the same as single gradient step. Our method extends the scope of existing LASSO algorithms to treat larger data sets, previously out of their reach. We show how our method can be extended to general l1 -penalized convex problems and present preliminary results for the Sparse Support Vector Machine and Logistic Regression problems.

Safe Feature Elimination in Sparse Supervised Learning

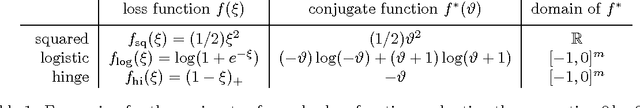
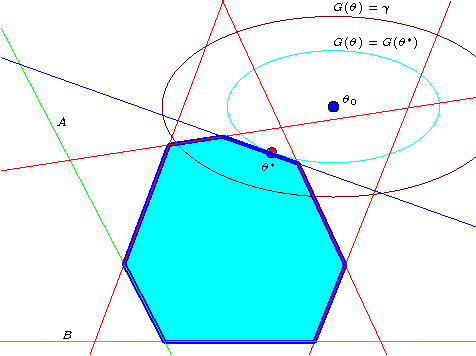
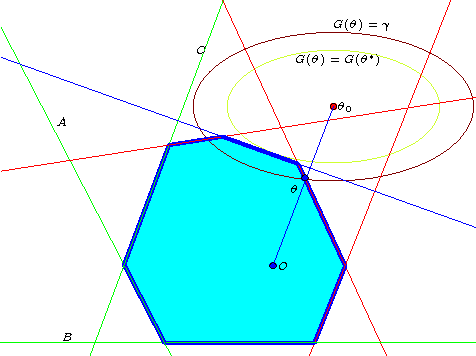
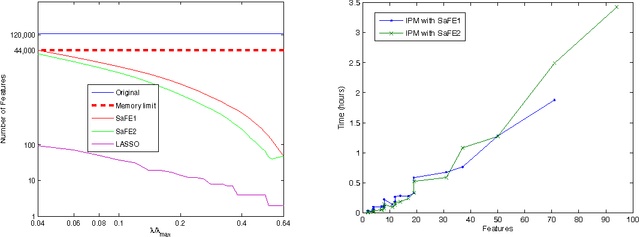
We investigate fast methods that allow to quickly eliminate variables (features) in supervised learning problems involving a convex loss function and a $l_1$-norm penalty, leading to a potentially substantial reduction in the number of variables prior to running the supervised learning algorithm. The methods are not heuristic: they only eliminate features that are {\em guaranteed} to be absent after solving the learning problem. Our framework applies to a large class of problems, including support vector machine classification, logistic regression and least-squares. The complexity of the feature elimination step is negligible compared to the typical computational effort involved in the sparse supervised learning problem: it grows linearly with the number of features times the number of examples, with much better count if data is sparse. We apply our method to data sets arising in text classification and observe a dramatic reduction of the dimensionality, hence in computational effort required to solve the learning problem, especially when very sparse classifiers are sought. Our method allows to immediately extend the scope of existing algorithms, allowing us to run them on data sets of sizes that were out of their reach before.

An empirical comparative study of approximate methods for binary graphical models; application to the search of associations among causes of death in French death certificates

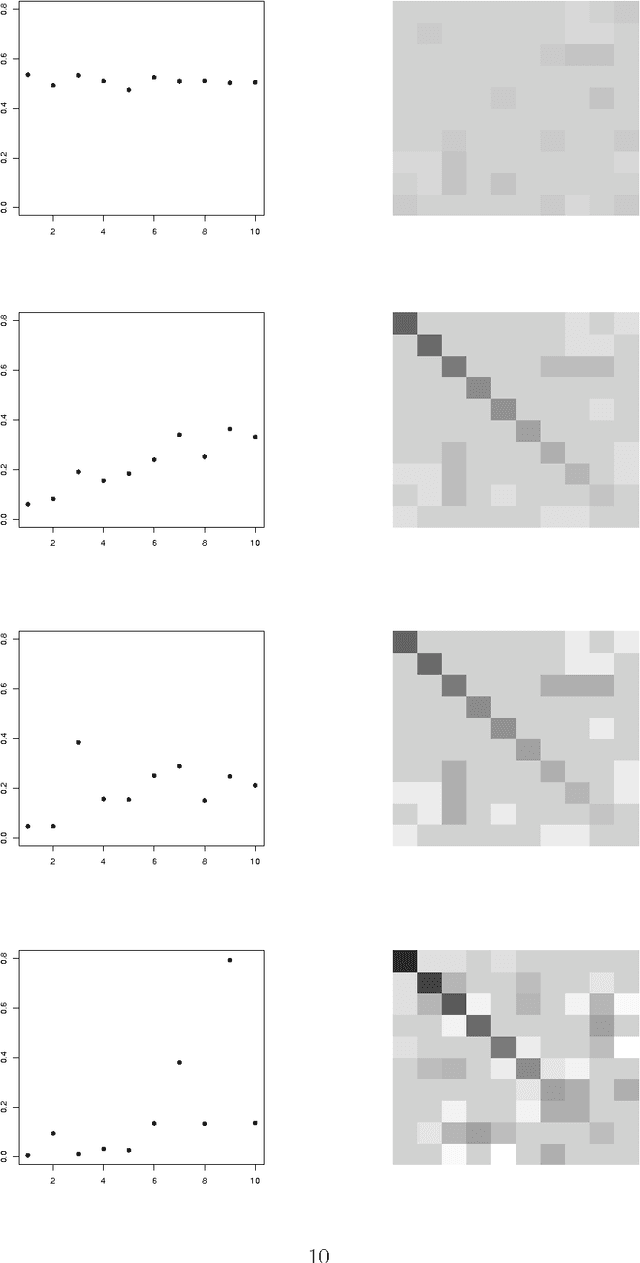
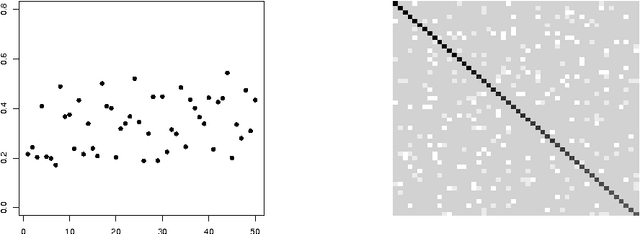
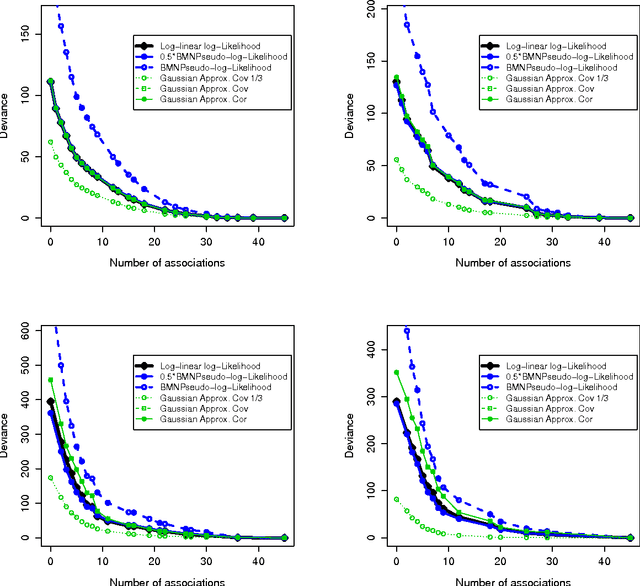
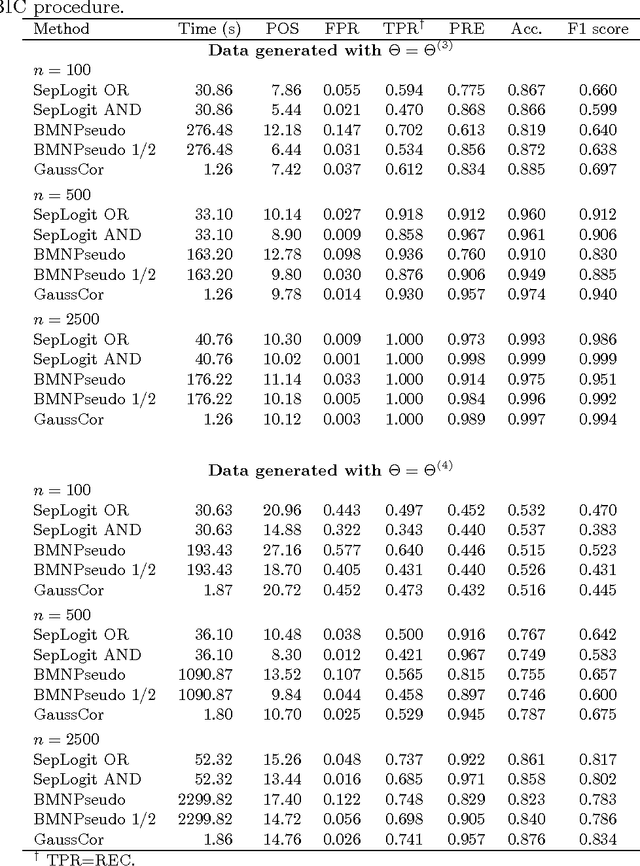
Looking for associations among multiple variables is a topical issue in statistics due to the increasing amount of data encountered in biology, medicine and many other domains involving statistical applications. Graphical models have recently gained popularity for this purpose in the statistical literature. Following the ideas of the LASSO procedure designed for the linear regression framework, recent developments dealing with graphical model selection have been based on $\ell_1$-penalization. In the binary case, however, exact inference is generally very slow or even intractable because of the form of the so-called log-partition function. Various approximate methods have recently been proposed in the literature and the main objective of this paper is to compare them. Through an extensive simulation study, we show that a simple modification of a method relying on a Gaussian approximation achieves good performance and is very fast. We present a real application in which we search for associations among causes of death recorded on French death certificates.