An empirical comparative study of approximate methods for binary graphical models; application to the search of associations among causes of death in French death certificates

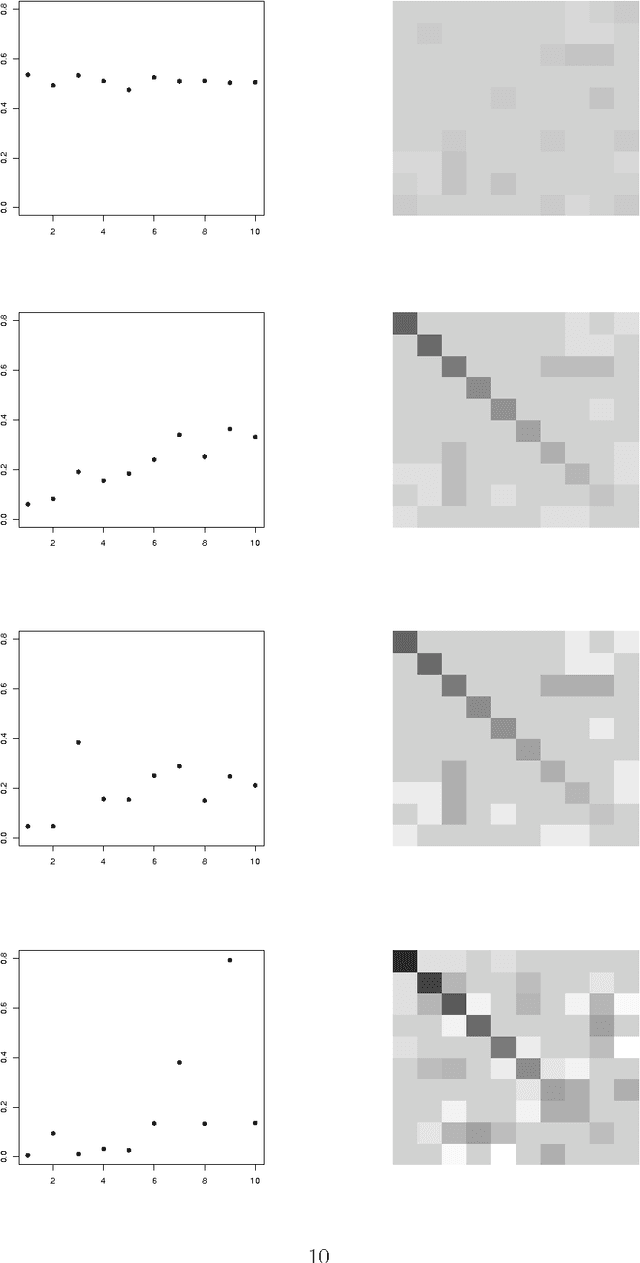
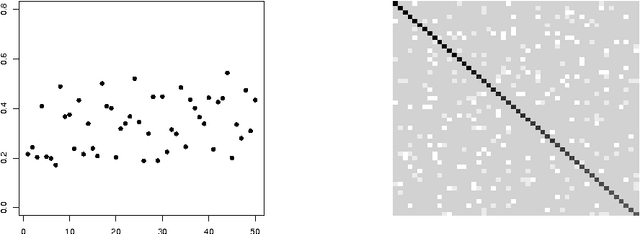
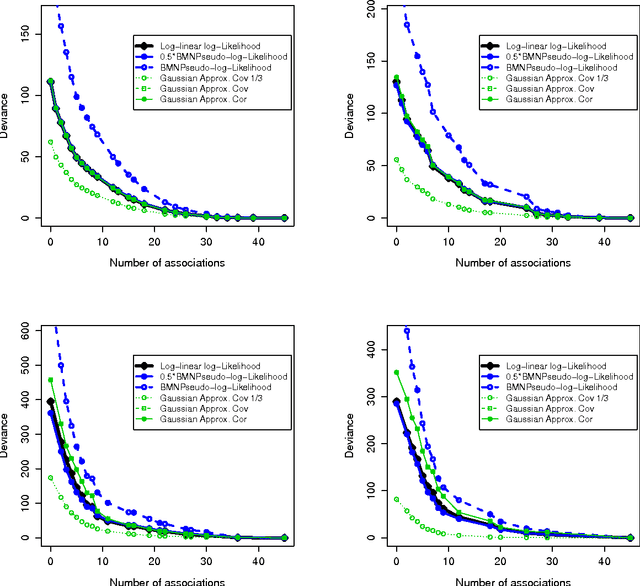
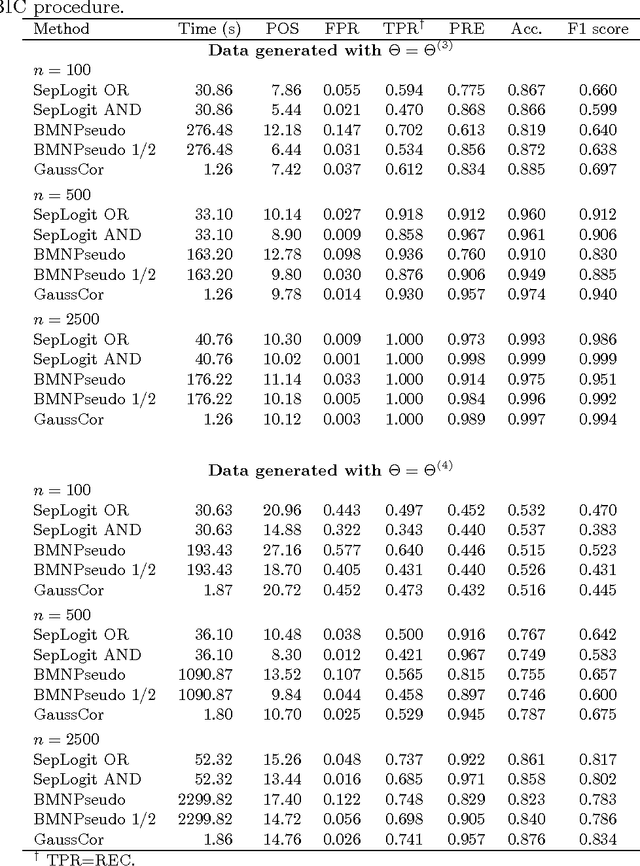
Looking for associations among multiple variables is a topical issue in statistics due to the increasing amount of data encountered in biology, medicine and many other domains involving statistical applications. Graphical models have recently gained popularity for this purpose in the statistical literature. Following the ideas of the LASSO procedure designed for the linear regression framework, recent developments dealing with graphical model selection have been based on $\ell_1$-penalization. In the binary case, however, exact inference is generally very slow or even intractable because of the form of the so-called log-partition function. Various approximate methods have recently been proposed in the literature and the main objective of this paper is to compare them. Through an extensive simulation study, we show that a simple modification of a method relying on a Gaussian approximation achieves good performance and is very fast. We present a real application in which we search for associations among causes of death recorded on French death certificates.

Model Selection Through Sparse Maximum Likelihood Estimation

We consider the problem of estimating the parameters of a Gaussian or binary distribution in such a way that the resulting undirected graphical model is sparse. Our approach is to solve a maximum likelihood problem with an added l_1-norm penalty term. The problem as formulated is convex but the memory requirements and complexity of existing interior point methods are prohibitive for problems with more than tens of nodes. We present two new algorithms for solving problems with at least a thousand nodes in the Gaussian case. Our first algorithm uses block coordinate descent, and can be interpreted as recursive l_1-norm penalized regression. Our second algorithm, based on Nesterov's first order method, yields a complexity estimate with a better dependence on problem size than existing interior point methods. Using a log determinant relaxation of the log partition function (Wainwright & Jordan (2006)), we show that these same algorithms can be used to solve an approximate sparse maximum likelihood problem for the binary case. We test our algorithms on synthetic data, as well as on gene expression and senate voting records data.

Sparse Covariance Selection via Robust Maximum Likelihood Estimation

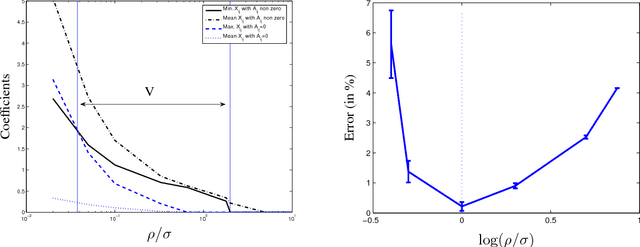
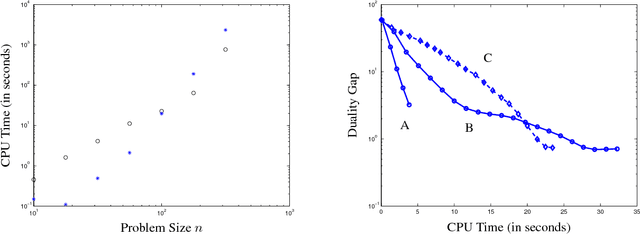
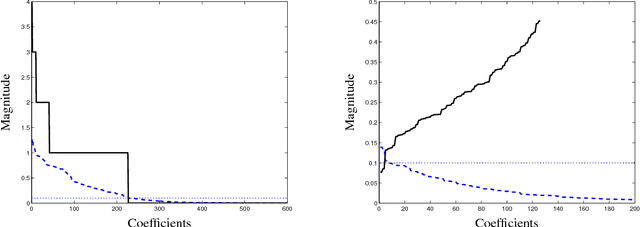
We address a problem of covariance selection, where we seek a trade-off between a high likelihood against the number of non-zero elements in the inverse covariance matrix. We solve a maximum likelihood problem with a penalty term given by the sum of absolute values of the elements of the inverse covariance matrix, and allow for imposing bounds on the condition number of the solution. The problem is directly amenable to now standard interior-point algorithms for convex optimization, but remains challenging due to its size. We first give some results on the theoretical computational complexity of the problem, by showing that a recent methodology for non-smooth convex optimization due to Nesterov can be applied to this problem, to greatly improve on the complexity estimate given by interior-point algorithms. We then examine two practical algorithms aimed at solving large-scale, noisy (hence dense) instances: one is based on a block-coordinate descent approach, where columns and rows are updated sequentially, another applies a dual version of Nesterov's method.