Safe Feature Elimination for the LASSO and Sparse Supervised Learning Problems
Paper and Code
May 18, 2011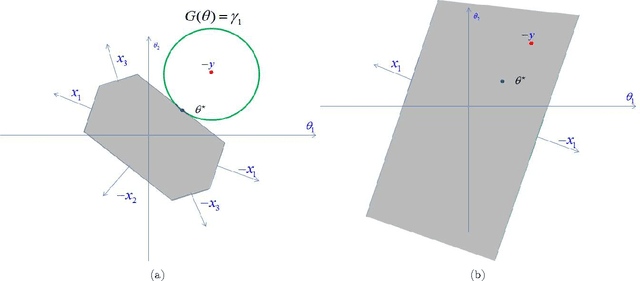
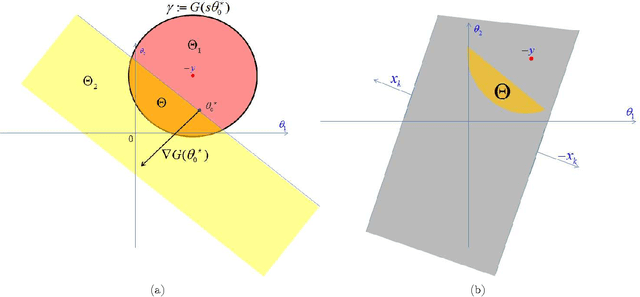
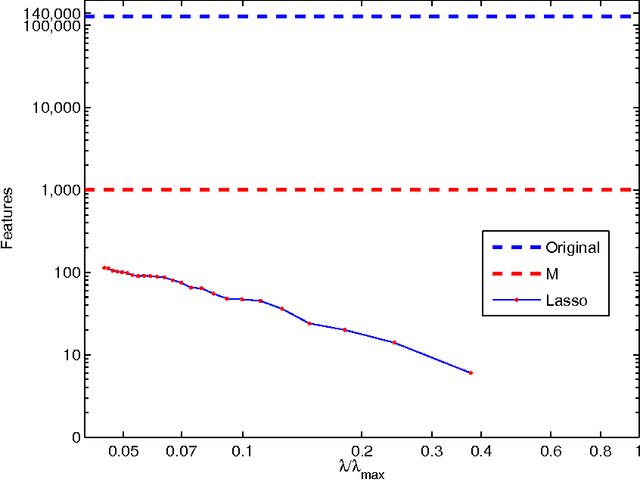
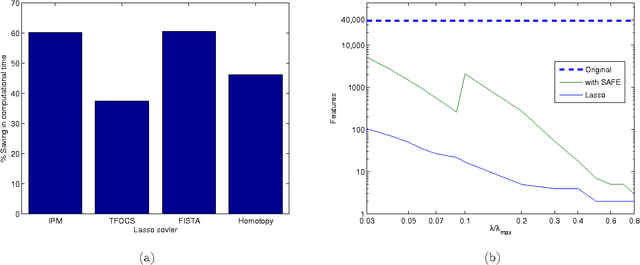
We describe a fast method to eliminate features (variables) in l1 -penalized least-square regression (or LASSO) problems. The elimination of features leads to a potentially substantial reduction in running time, specially for large values of the penalty parameter. Our method is not heuristic: it only eliminates features that are guaranteed to be absent after solving the LASSO problem. The feature elimination step is easy to parallelize and can test each feature for elimination independently. Moreover, the computational effort of our method is negligible compared to that of solving the LASSO problem - roughly it is the same as single gradient step. Our method extends the scope of existing LASSO algorithms to treat larger data sets, previously out of their reach. We show how our method can be extended to general l1 -penalized convex problems and present preliminary results for the Sparse Support Vector Machine and Logistic Regression problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge