Safe Feature Elimination in Sparse Supervised Learning
Paper and Code
Oct 26, 2010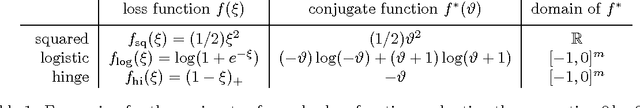
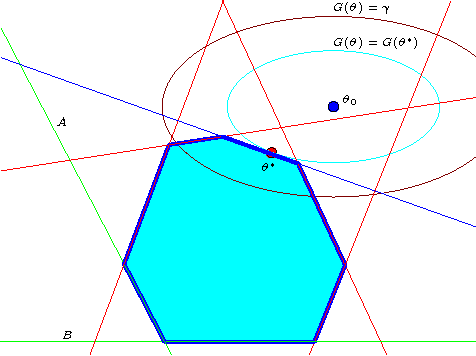
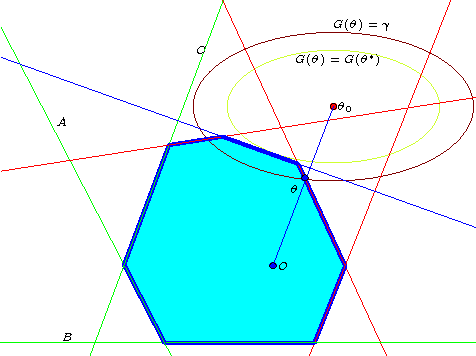
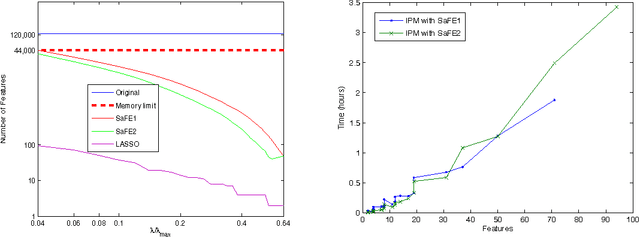
We investigate fast methods that allow to quickly eliminate variables (features) in supervised learning problems involving a convex loss function and a $l_1$-norm penalty, leading to a potentially substantial reduction in the number of variables prior to running the supervised learning algorithm. The methods are not heuristic: they only eliminate features that are {\em guaranteed} to be absent after solving the learning problem. Our framework applies to a large class of problems, including support vector machine classification, logistic regression and least-squares. The complexity of the feature elimination step is negligible compared to the typical computational effort involved in the sparse supervised learning problem: it grows linearly with the number of features times the number of examples, with much better count if data is sparse. We apply our method to data sets arising in text classification and observe a dramatic reduction of the dimensionality, hence in computational effort required to solve the learning problem, especially when very sparse classifiers are sought. Our method allows to immediately extend the scope of existing algorithms, allowing us to run them on data sets of sizes that were out of their reach before.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge