Learning Energy-Based Models by Self-normalising the Likelihood

Training an energy-based model (EBM) with maximum likelihood is challenging due to the intractable normalisation constant. Traditional methods rely on expensive Markov chain Monte Carlo (MCMC) sampling to estimate the gradient of logartihm of the normalisation constant. We propose a novel objective called self-normalised log-likelihood (SNL) that introduces a single additional learnable parameter representing the normalisation constant compared to the regular log-likelihood. SNL is a lower bound of the log-likelihood, and its optimum corresponds to both the maximum likelihood estimate of the model parameters and the normalisation constant. We show that the SNL objective is concave in the model parameters for exponential family distributions. Unlike the regular log-likelihood, the SNL can be directly optimised using stochastic gradient techniques by sampling from a crude proposal distribution. We validate the effectiveness of our proposed method on various density estimation tasks as well as EBMs for regression. Our results show that the proposed method, while simpler to implement and tune, outperforms existing techniques.

Debiasing Guidance for Discrete Diffusion with Sequential Monte Carlo

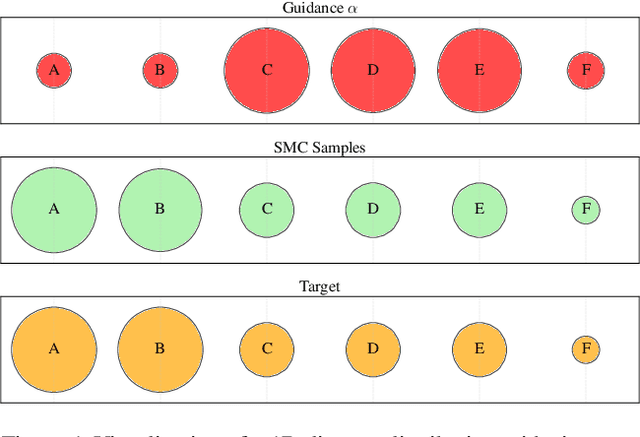
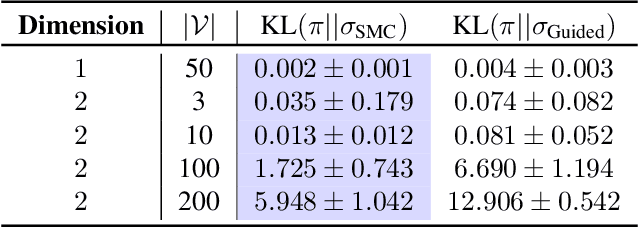
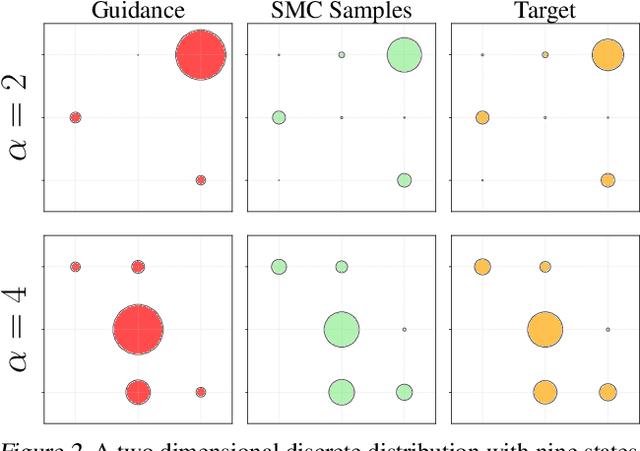
Discrete diffusion models are a class of generative models that produce samples from an approximated data distribution within a discrete state space. Often, there is a need to target specific regions of the data distribution. Current guidance methods aim to sample from a distribution with mass proportional to $p_0(x_0) p(\zeta|x_0)^\alpha$ but fail to achieve this in practice. We introduce a Sequential Monte Carlo algorithm that generates unbiasedly from this target distribution, utilising the learnt unconditional and guided process. We validate our approach on low-dimensional distributions, controlled images and text generations. For text generation, our method provides strong control while maintaining low perplexity compared to guidance-based approaches.

Generative Diffusion Models for Sequential Recommendations

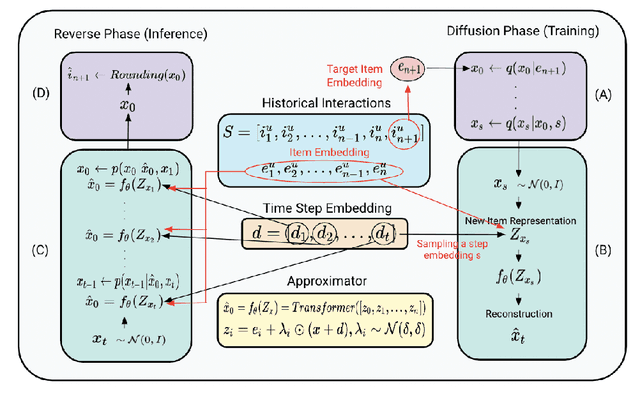
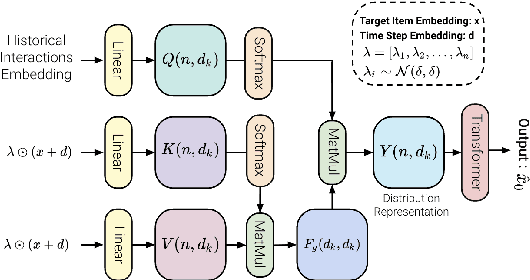
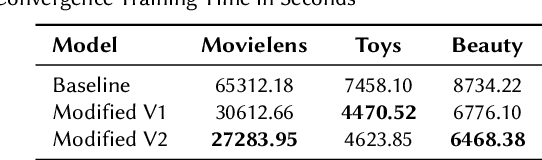
Generative models such as Variational Autoencoders (VAEs) and Generative Adversarial Networks (GANs) have shown promise in sequential recommendation tasks. However, they face challenges, including posterior collapse and limited representation capacity. The work by Li et al. (2023) introduces a novel approach that leverages diffusion models to address these challenges by representing item embeddings as distributions rather than fixed vectors. This approach allows for a more adaptive reflection of users' diverse interests and various item aspects. During the diffusion phase, the model converts the target item embedding into a Gaussian distribution by adding noise, facilitating the representation of sequential item distributions and the injection of uncertainty. An Approximator then processes this noisy item representation to reconstruct the target item. In the reverse phase, the model utilizes users' past interactions to reverse the noise and finalize the item prediction through a rounding operation. This research introduces enhancements to the DiffuRec architecture, particularly by adding offset noise in the diffusion process to improve robustness and incorporating a cross-attention mechanism in the Approximator to better capture relevant user-item interactions. These contributions led to the development of a new model, DiffuRecSys, which improves performance. Extensive experiments conducted on three public benchmark datasets demonstrate that these modifications enhance item representation, effectively capture diverse user preferences, and outperform existing baselines in sequential recommendation research.

Variance reduction of diffusion model's gradients with Taylor approximation-based control variate

Score-based models, trained with denoising score matching, are remarkably effective in generating high dimensional data. However, the high variance of their training objective hinders optimisation. We attempt to reduce it with a control variate, derived via a $k$-th order Taylor expansion on the training objective and its gradient. We prove an equivalence between the two and demonstrate empirically the effectiveness of our approach on a low dimensional problem setting; and study its effect on larger problems.