Food for thought: How can machine learning help better predict and understand changes in food prices?

In this work, we address a lack of systematic understanding of fluctuations in food affordability in Canada. Canada's Food Price Report (CPFR) is an annual publication that predicts food inflation over the next calendar year. The published predictions are a collaborative effort between forecasting teams that each employ their own approach at Canadian Universities: Dalhousie University, the University of British Columbia, the University of Saskatchewan, and the University of Guelph/Vector Institute. While the University of Guelph/Vector Institute forecasting team has leveraged machine learning (ML) in previous reports, the most recent editions (2024--2025) have also included a human-in-the-loop approach. For the 2025 report, this focus was expanded to evaluate several different data-centric approaches to improve forecast accuracy. In this study, we evaluate how different types of forecasting models perform when estimating food price fluctuations. We also examine the sensitivity of models that curate time series data representing key factors in food pricing.

Autoregressive Conditional Neural Processes

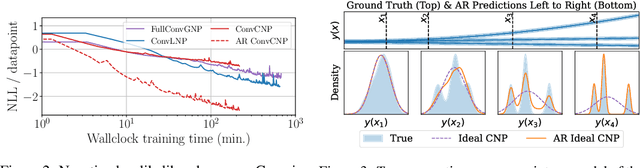
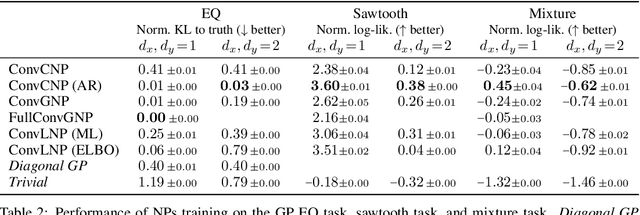
Conditional neural processes (CNPs; Garnelo et al., 2018a) are attractive meta-learning models which produce well-calibrated predictions and are trainable via a simple maximum likelihood procedure. Although CNPs have many advantages, they are unable to model dependencies in their predictions. Various works propose solutions to this, but these come at the cost of either requiring approximate inference or being limited to Gaussian predictions. In this work, we instead propose to change how CNPs are deployed at test time, without any modifications to the model or training procedure. Instead of making predictions independently for every target point, we autoregressively define a joint predictive distribution using the chain rule of probability, taking inspiration from the neural autoregressive density estimator (NADE) literature. We show that this simple procedure allows factorised Gaussian CNPs to model highly dependent, non-Gaussian predictive distributions. Perhaps surprisingly, in an extensive range of tasks with synthetic and real data, we show that CNPs in autoregressive (AR) mode not only significantly outperform non-AR CNPs, but are also competitive with more sophisticated models that are significantly more computationally expensive and challenging to train. This performance is remarkable given that AR CNPs are not trained to model joint dependencies. Our work provides an example of how ideas from neural distribution estimation can benefit neural processes, and motivates research into the AR deployment of other neural process models.