Optimization Algorithm Design via Electric Circuits

We present a novel methodology for convex optimization algorithm design using ideas from electric RLC circuits. Given an optimization problem, the first stage of the methodology is to design an appropriate electric circuit whose continuous-time dynamics converge to the solution of the optimization problem at hand. Then, the second stage is an automated, computer-assisted discretization of the continuous-time dynamics, yielding a provably convergent discrete-time algorithm. Our methodology recovers many classical (distributed) optimization algorithms and enables users to quickly design and explore a wide range of new algorithms with convergence guarantees.

Fitting Multilevel Factor Models

We examine a special case of the multilevel factor model, with covariance given by multilevel low rank (MLR) matrix~\cite{parshakova2023factor}. We develop a novel, fast implementation of the expectation-maximization (EM) algorithm, tailored for multilevel factor models, to maximize the likelihood of the observed data. This method accommodates any hierarchical structure and maintains linear time and storage complexities per iteration. This is achieved through a new efficient technique for computing the inverse of the positive definite MLR matrix. We show that the inverse of an invertible PSD MLR matrix is also an MLR matrix with the same sparsity in factors, and we use the recursive Sherman-Morrison-Woodbury matrix identity to obtain the factors of the inverse. Additionally, we present an algorithm that computes the Cholesky factorization of an expanded matrix with linear time and space complexities, yielding the covariance matrix as its Schur complement. This paper is accompanied by an open-source package that implements the proposed methods.

Factor Fitting, Rank Allocation, and Partitioning in Multilevel Low Rank Matrices

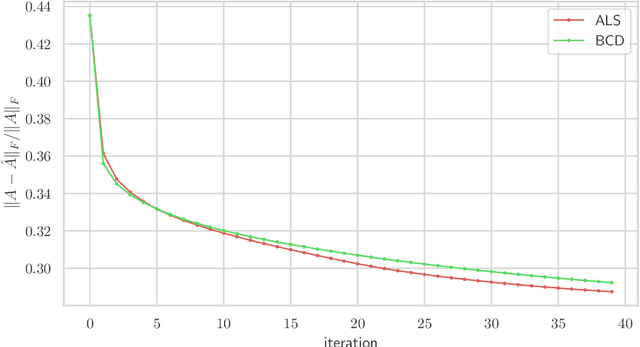
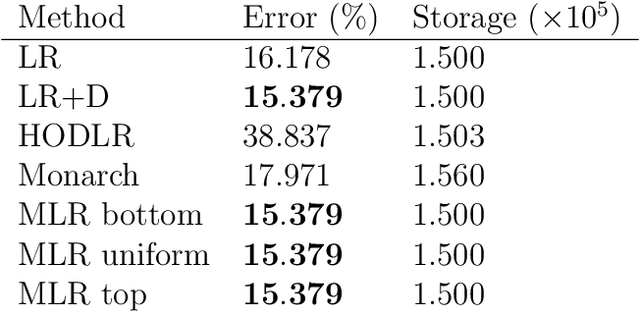
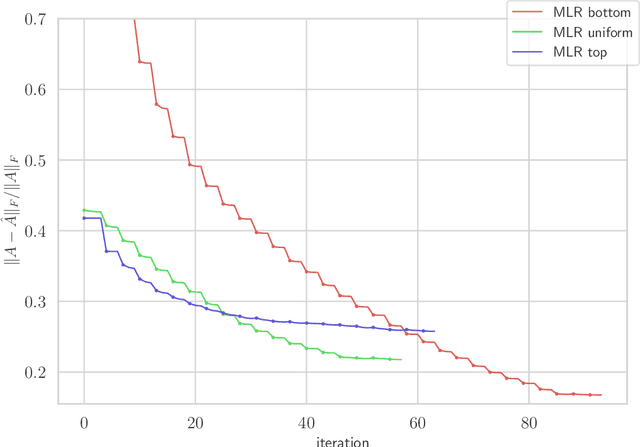
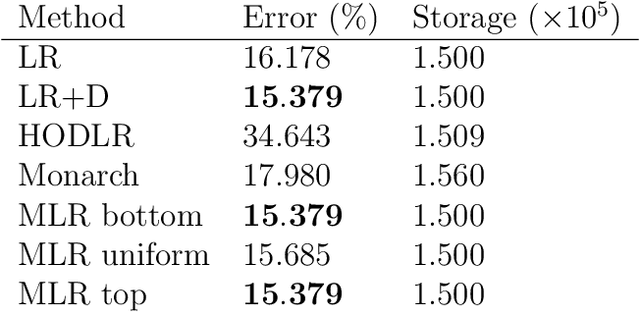
We consider multilevel low rank (MLR) matrices, defined as a row and column permutation of a sum of matrices, each one a block diagonal refinement of the previous one, with all blocks low rank given in factored form. MLR matrices extend low rank matrices but share many of their properties, such as the total storage required and complexity of matrix-vector multiplication. We address three problems that arise in fitting a given matrix by an MLR matrix in the Frobenius norm. The first problem is factor fitting, where we adjust the factors of the MLR matrix. The second is rank allocation, where we choose the ranks of the blocks in each level, subject to the total rank having a given value, which preserves the total storage needed for the MLR matrix. The final problem is to choose the hierarchical partition of rows and columns, along with the ranks and factors. This paper is accompanied by an open source package that implements the proposed methods.

Efficient Graph Field Integrators Meet Point Clouds

We present two new classes of algorithms for efficient field integration on graphs encoding point clouds. The first class, SeparatorFactorization(SF), leverages the bounded genus of point cloud mesh graphs, while the second class, RFDiffusion(RFD), uses popular epsilon-nearest-neighbor graph representations for point clouds. Both can be viewed as providing the functionality of Fast Multipole Methods (FMMs), which have had a tremendous impact on efficient integration, but for non-Euclidean spaces. We focus on geometries induced by distributions of walk lengths between points (e.g., shortest-path distance). We provide an extensive theoretical analysis of our algorithms, obtaining new results in structural graph theory as a byproduct. We also perform exhaustive empirical evaluation, including on-surface interpolation for rigid and deformable objects (particularly for mesh-dynamics modeling), Wasserstein distance computations for point clouds, and the Gromov-Wasserstein variant.

Distributional Reinforcement Learning for Energy-Based Sequential Models

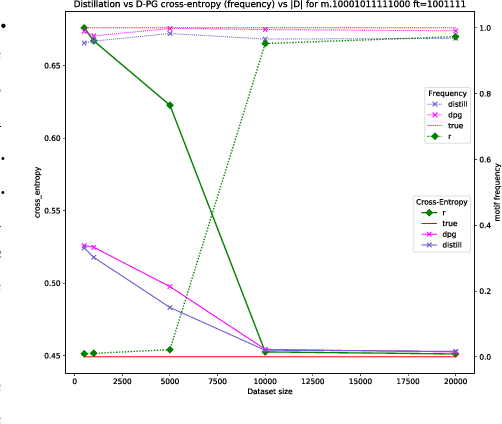
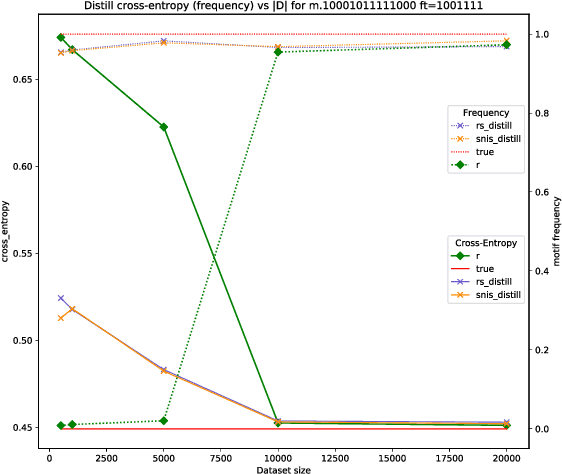
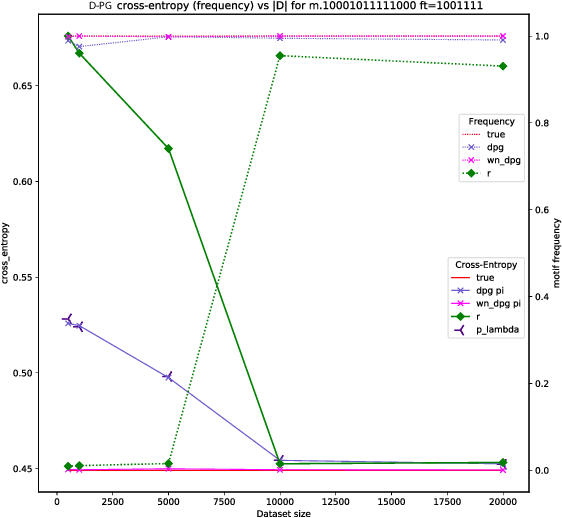
Global Autoregressive Models (GAMs) are a recent proposal [Parshakova et al., CoNLL 2019] for exploiting global properties of sequences for data-efficient learning of seq2seq models. In the first phase of training, an Energy-Based model (EBM) over sequences is derived. This EBM has high representational power, but is unnormalized and cannot be directly exploited for sampling. To address this issue [Parshakova et al., CoNLL 2019] proposes a distillation technique, which can only be applied under limited conditions. By relating this problem to Policy Gradient techniques in RL, but in a \emph{distributional} rather than \emph{optimization} perspective, we propose a general approach applicable to any sequential EBM. Its effectiveness is illustrated on GAM-based experiments.

Global Autoregressive Models for Data-Efficient Sequence Learning

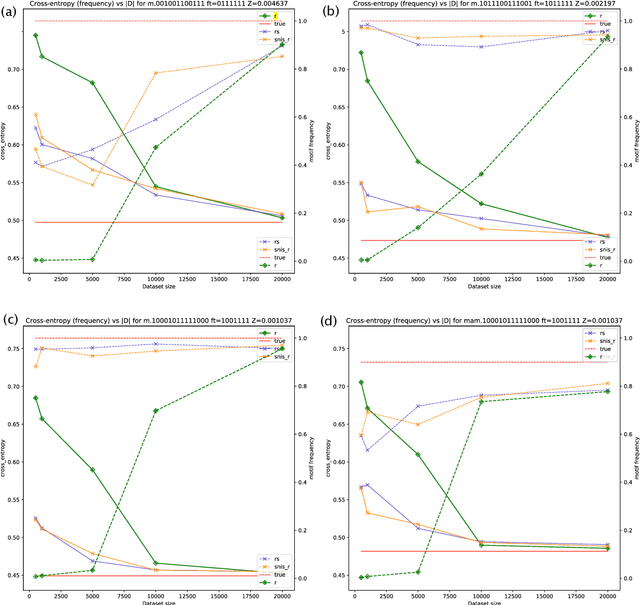
Standard autoregressive seq2seq models are easily trained by max-likelihood, but tend to show poor results under small-data conditions. We introduce a class of seq2seq models, GAMs (Global Autoregressive Models), which combine an autoregressive component with a log-linear component, allowing the use of global \textit{a priori} features to compensate for lack of data. We train these models in two steps. In the first step, we obtain an \emph{unnormalized} GAM that maximizes the likelihood of the data, but is improper for fast inference or evaluation. In the second step, we use this GAM to train (by distillation) a second autoregressive model that approximates the \emph{normalized} distribution associated with the GAM, and can be used for fast inference and evaluation. Our experiments focus on language modelling under synthetic conditions and show a strong perplexity reduction of using the second autoregressive model over the standard one.