Optimization Algorithm Design via Electric Circuits

We present a novel methodology for convex optimization algorithm design using ideas from electric RLC circuits. Given an optimization problem, the first stage of the methodology is to design an appropriate electric circuit whose continuous-time dynamics converge to the solution of the optimization problem at hand. Then, the second stage is an automated, computer-assisted discretization of the continuous-time dynamics, yielding a provably convergent discrete-time algorithm. Our methodology recovers many classical (distributed) optimization algorithms and enables users to quickly design and explore a wide range of new algorithms with convergence guarantees.

Model-Based Deep Learning: On the Intersection of Deep Learning and Optimization

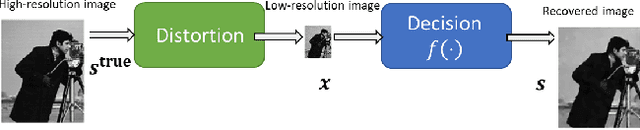
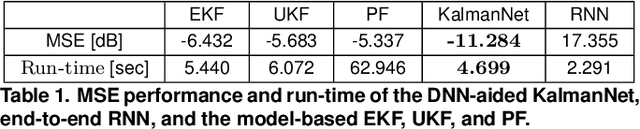
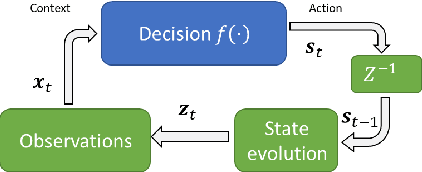
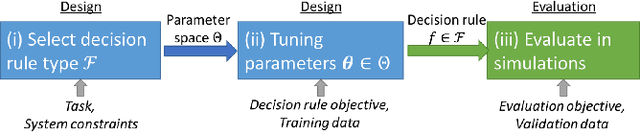
Decision making algorithms are used in a multitude of different applications. Conventional approaches for designing decision algorithms employ principled and simplified modelling, based on which one can determine decisions via tractable optimization. More recently, deep learning approaches that use highly parametric architectures tuned from data without relying on mathematical models, are becoming increasingly popular. Model-based optimization and data-centric deep learning are often considered to be distinct disciplines. Here, we characterize them as edges of a continuous spectrum varying in specificity and parameterization, and provide a tutorial-style presentation to the methodologies lying in the middle ground of this spectrum, referred to as model-based deep learning. We accompany our presentation with running examples in super-resolution and stochastic control, and show how they are expressed using the provided characterization and specialized in each of the detailed methodologies. The gains of combining model-based optimization and deep learning are demonstrated using experimental results in various applications, ranging from biomedical imaging to digital communications.

Signal Decomposition Using Masked Proximal Operators

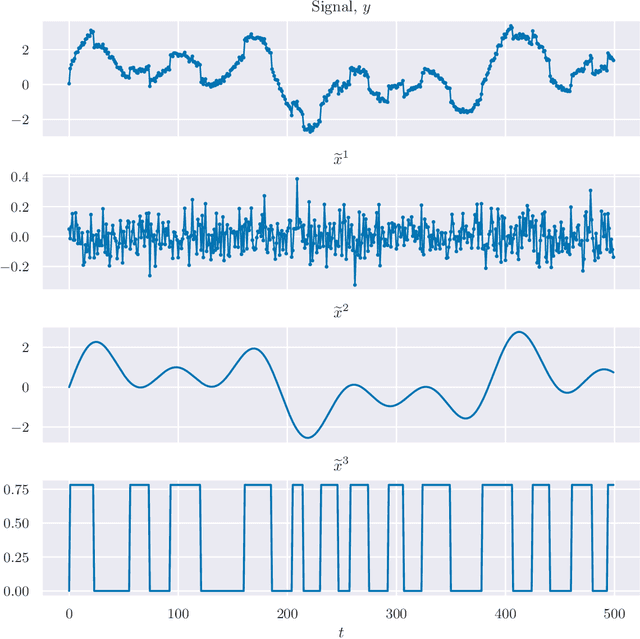
We consider the well-studied problem of decomposing a vector time series signal into components with different characteristics, such as smooth, periodic, nonnegative, or sparse. We propose a simple and general framework in which the components are defined by loss functions (which include constraints), and the signal decomposition is carried out by minimizing the sum of losses of the components (subject to the constraints). When each loss function is the negative log-likelihood of a density for the signal component, our method coincides with maximum a posteriori probability (MAP) estimation; but it also includes many other interesting cases. We give two distributed optimization methods for computing the decomposition, which find the optimal decomposition when the component class loss functions are convex, and are good heuristics when they are not. Both methods require only the masked proximal operator of each of the component loss functions, a generalization of the well-known proximal operator that handles missing entries in its argument. Both methods are distributed, i.e., handle each component separately. We derive tractable methods for evaluating the masked proximal operators of some loss functions that, to our knowledge, have not appeared in the literature.