Bennet E. Meyers
Signal Decomposition Using Masked Proximal Operators
Mar 02, 2022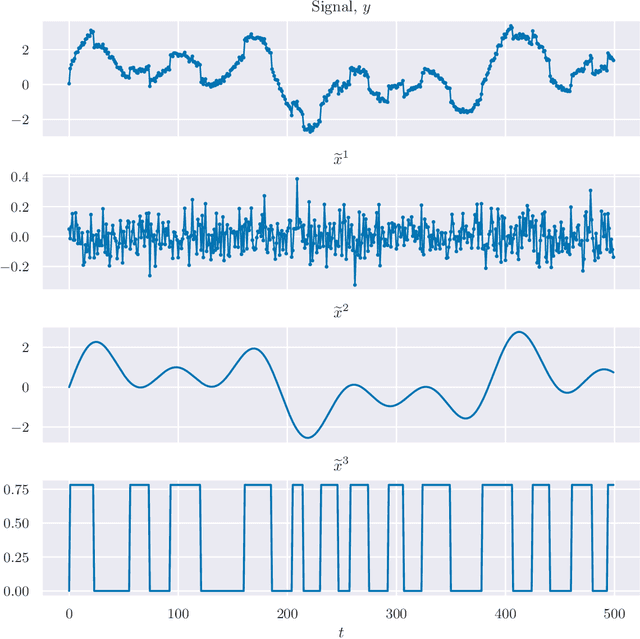
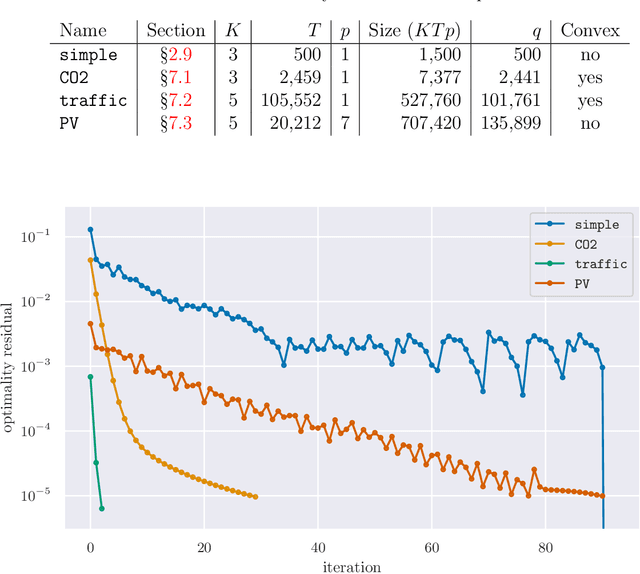
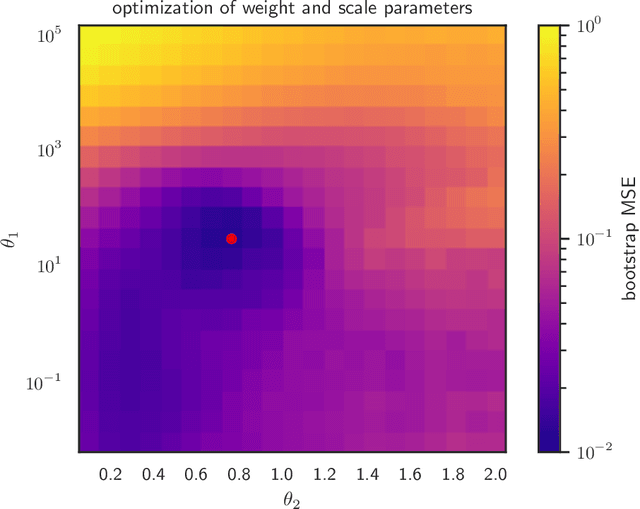
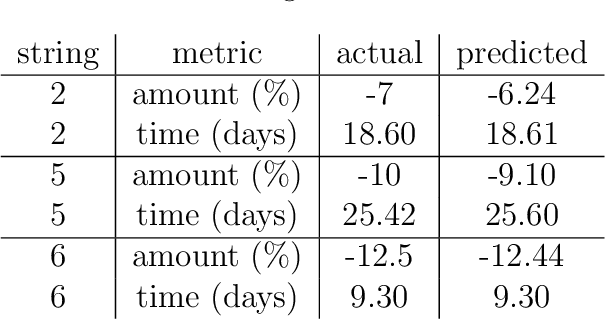
Abstract:We consider the well-studied problem of decomposing a vector time series signal into components with different characteristics, such as smooth, periodic, nonnegative, or sparse. We propose a simple and general framework in which the components are defined by loss functions (which include constraints), and the signal decomposition is carried out by minimizing the sum of losses of the components (subject to the constraints). When each loss function is the negative log-likelihood of a density for the signal component, our method coincides with maximum a posteriori probability (MAP) estimation; but it also includes many other interesting cases. We give two distributed optimization methods for computing the decomposition, which find the optimal decomposition when the component class loss functions are convex, and are good heuristics when they are not. Both methods require only the masked proximal operator of each of the component loss functions, a generalization of the well-known proximal operator that handles missing entries in its argument. Both methods are distributed, i.e., handle each component separately. We derive tractable methods for evaluating the masked proximal operators of some loss functions that, to our knowledge, have not appeared in the literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge