Global Autoregressive Models for Data-Efficient Sequence Learning
Paper and Code
Sep 19, 2019

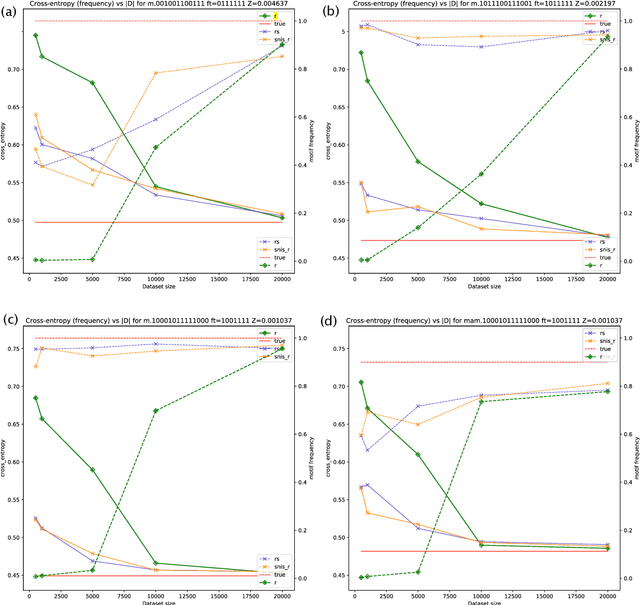
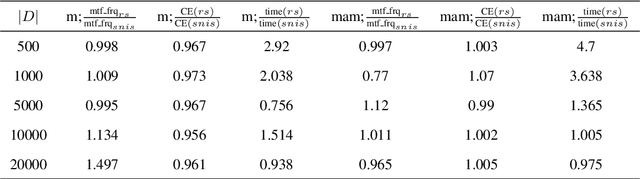
Standard autoregressive seq2seq models are easily trained by max-likelihood, but tend to show poor results under small-data conditions. We introduce a class of seq2seq models, GAMs (Global Autoregressive Models), which combine an autoregressive component with a log-linear component, allowing the use of global \textit{a priori} features to compensate for lack of data. We train these models in two steps. In the first step, we obtain an \emph{unnormalized} GAM that maximizes the likelihood of the data, but is improper for fast inference or evaluation. In the second step, we use this GAM to train (by distillation) a second autoregressive model that approximates the \emph{normalized} distribution associated with the GAM, and can be used for fast inference and evaluation. Our experiments focus on language modelling under synthetic conditions and show a strong perplexity reduction of using the second autoregressive model over the standard one.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge