A Planning Framework for Adaptive Labeling

Ground truth labels/outcomes are critical for advancing scientific and engineering applications, e.g., evaluating the treatment effect of an intervention or performance of a predictive model. Since randomly sampling inputs for labeling can be prohibitively expensive, we introduce an adaptive labeling framework where measurement effort can be reallocated in batches. We formulate this problem as a Markov decision process where posterior beliefs evolve over time as batches of labels are collected (state transition), and batches (actions) are chosen to minimize uncertainty at the end of data collection. We design a computational framework that is agnostic to different uncertainty quantification approaches including those based on deep learning, and allows a diverse array of policy gradient approaches by relying on continuous policy parameterizations. On real and synthetic datasets, we demonstrate even a one-step lookahead policy can substantially outperform common adaptive labeling heuristics, highlighting the virtue of planning. On the methodological side, we note that standard REINFORCE-style policy gradient estimators can suffer high variance since they rely only on zeroth order information. We propose a direct backpropagation-based approach, Smoothed-Autodiff, based on a carefully smoothed version of the original non-differentiable MDP. Our method enjoys low variance at the price of introducing bias, and we theoretically and empirically show that this trade-off can be favorable.

Minimax Optimal Estimation of Stability Under Distribution Shift

The performance of decision policies and prediction models often deteriorates when applied to environments different from the ones seen during training. To ensure reliable operation, we propose and analyze the stability of a system under distribution shift, which is defined as the smallest change in the underlying environment that causes the system's performance to deteriorate beyond a permissible threshold. In contrast to standard tail risk measures and distributionally robust losses that require the specification of a plausible magnitude of distribution shift, the stability measure is defined in terms of a more intuitive quantity: the level of acceptable performance degradation. We develop a minimax optimal estimator of stability and analyze its convergence rate, which exhibits a fundamental phase shift behavior. Our characterization of the minimax convergence rate shows that evaluating stability against large performance degradation incurs a statistical cost. Empirically, we demonstrate the practical utility of our stability framework by using it to compare system designs on problems where robustness to distribution shift is critical.

Hybrid Random Features

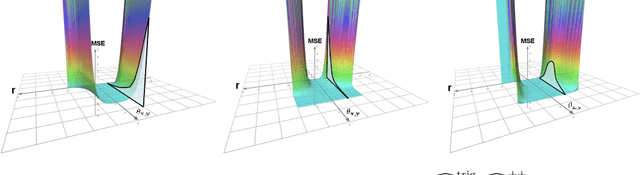
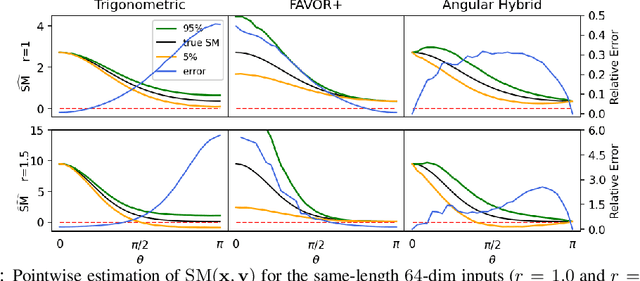
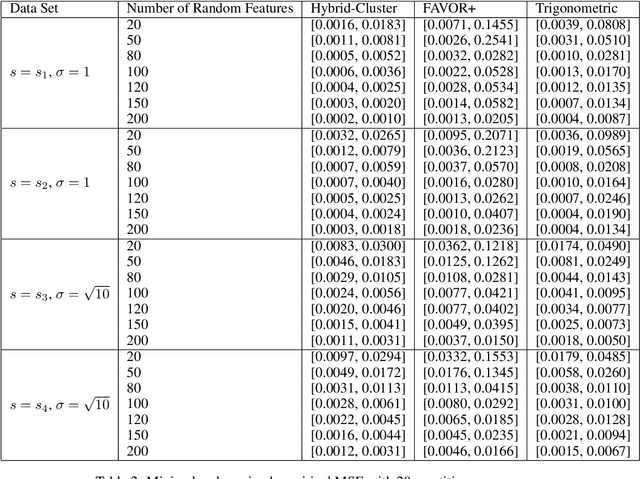
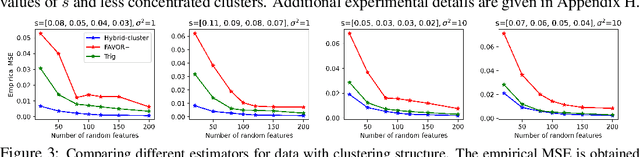
We propose a new class of random feature methods for linearizing softmax and Gaussian kernels called hybrid random features (HRFs) that automatically adapt the quality of kernel estimation to provide most accurate approximation in the defined regions of interest. Special instantiations of HRFs lead to well-known methods such as trigonometric (Rahimi and Recht, 2007) or (recently introduced in the context of linear-attention Transformers) positive random features (Choromanski et al., 2021). By generalizing Bochner's Theorem for softmax/Gaussian kernels and leveraging random features for compositional kernels, the HRF-mechanism provides strong theoretical guarantees - unbiased approximation and strictly smaller worst-case relative errors than its counterparts. We conduct exhaustive empirical evaluation of HRF ranging from pointwise kernel estimation experiments, through tests on data admitting clustering structure to benchmarking implicit-attention Transformers (also for downstream Robotics applications), demonstrating its quality in a wide spectrum of machine learning problems.