Online Linear Programming with Batching

We study Online Linear Programming (OLP) with batching. The planning horizon is cut into $K$ batches, and the decisions on customers arriving within a batch can be delayed to the end of their associated batch. Compared with OLP without batching, the ability to delay decisions brings better operational performance, as measured by regret. Two research questions of interest are: (1) What is a lower bound of the regret as a function of $K$? (2) What algorithms can achieve the regret lower bound? These questions have been analyzed in the literature when the distribution of the reward and the resource consumption of the customers have finite support. By contrast, this paper analyzes these questions when the conditional distribution of the reward given the resource consumption is continuous, and we show the answers are different under this setting. When there is only a single type of resource and the decision maker knows the total number of customers, we propose an algorithm with a $O(\log K)$ regret upper bound and provide a $\Omega(\log K)$ regret lower bound. We also propose algorithms with $O(\log K)$ regret upper bound for the setting in which there are multiple types of resource and the setting in which customers arrive following a Poisson process. All these regret upper and lower bounds are independent of the length of the planning horizon, and all the proposed algorithms delay decisions on customers arriving in only the first and the last batch. We also take customer impatience into consideration and establish a way of selecting an appropriate batch size.

Overlapping Batch Confidence Intervals on Statistical Functionals Constructed from Time Series: Application to Quantiles, Optimization, and Estimation

We propose a general purpose confidence interval procedure (CIP) for statistical functionals constructed using data from a stationary time series. The procedures we propose are based on derived distribution-free analogues of the $\chi^2$ and Student's $t$ random variables for the statistical functional context, and hence apply in a wide variety of settings including quantile estimation, gradient estimation, M-estimation, CVAR-estimation, and arrival process rate estimation, apart from more traditional statistical settings. Like the method of subsampling, we use overlapping batches of time series data to estimate the underlying variance parameter; unlike subsampling and the bootstrap, however, we assume that the implied point estimator of the statistical functional obeys a central limit theorem (CLT) to help identify the weak asymptotics (called OB-x limits, x=I,II,III) of batched Studentized statistics. The OB-x limits, certain functionals of the Wiener process parameterized by the size of the batches and the extent of their overlap, form the essential machinery for characterizing dependence, and consequently the correctness of the proposed CIPs. The message from extensive numerical experimentation is that in settings where a functional CLT on the point estimator is in effect, using \emph{large overlapping batches} alongside OB-x critical values yields confidence intervals that are often of significantly higher quality than those obtained from more generic methods like subsampling or the bootstrap. We illustrate using examples from CVaR estimation, ARMA parameter estimation, and NHPP rate estimation; R and MATLAB code for OB-x critical values is available at~\texttt{web.ics.purdue.edu/~pasupath/}.

Minimax Optimal Estimation of Stability Under Distribution Shift

The performance of decision policies and prediction models often deteriorates when applied to environments different from the ones seen during training. To ensure reliable operation, we propose and analyze the stability of a system under distribution shift, which is defined as the smallest change in the underlying environment that causes the system's performance to deteriorate beyond a permissible threshold. In contrast to standard tail risk measures and distributionally robust losses that require the specification of a plausible magnitude of distribution shift, the stability measure is defined in terms of a more intuitive quantity: the level of acceptable performance degradation. We develop a minimax optimal estimator of stability and analyze its convergence rate, which exhibits a fundamental phase shift behavior. Our characterization of the minimax convergence rate shows that evaluating stability against large performance degradation incurs a statistical cost. Empirically, we demonstrate the practical utility of our stability framework by using it to compare system designs on problems where robustness to distribution shift is critical.

Risk-Sensitive Markov Decision Processes with Long-Run CVaR Criterion

CVaR (Conditional Value at Risk) is a risk metric widely used in finance. However, dynamically optimizing CVaR is difficult since it is not a standard Markov decision process (MDP) and the principle of dynamic programming fails. In this paper, we study the infinite-horizon discrete-time MDP with a long-run CVaR criterion, from the view of sensitivity-based optimization. By introducing a pseudo CVaR metric, we derive a CVaR difference formula which quantifies the difference of long-run CVaR under any two policies. The optimality of deterministic policies is derived. We obtain a so-called Bellman local optimality equation for CVaR, which is a necessary and sufficient condition for local optimal policies and only necessary for global optimal policies. A CVaR derivative formula is also derived for providing more sensitivity information. Then we develop a policy iteration type algorithm to efficiently optimize CVaR, which is shown to converge to local optima in the mixed policy space. We further discuss some extensions including the mean-CVaR optimization and the maximization of CVaR. Finally, we conduct numerical experiments relating to portfolio management to demonstrate the main results. Our work may shed light on dynamically optimizing CVaR from a sensitivity viewpoint.

The Typical Behavior of Bandit Algorithms

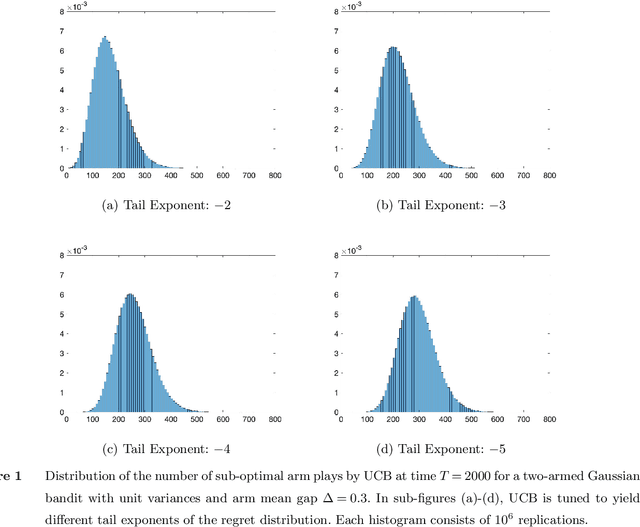
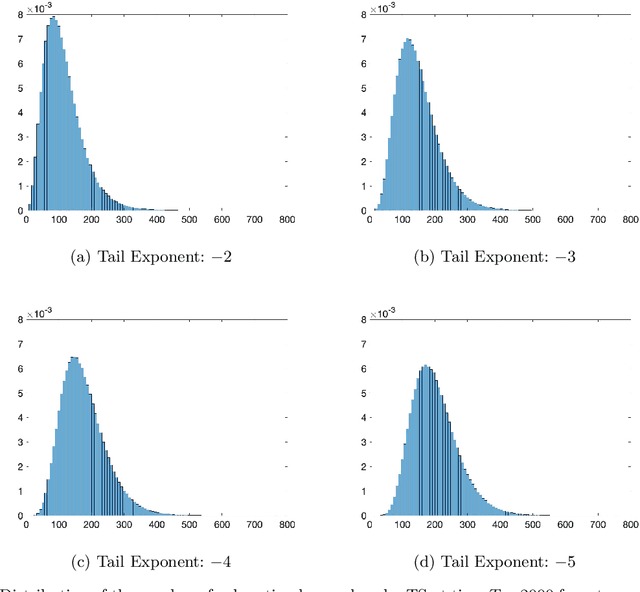
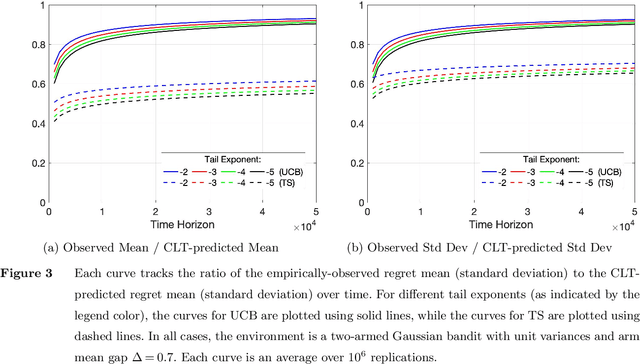
We establish strong laws of large numbers and central limit theorems for the regret of two of the most popular bandit algorithms: Thompson sampling and UCB. Here, our characterizations of the regret distribution complement the characterizations of the tail of the regret distribution recently developed by Fan and Glynn (2021) (arXiv:2109.13595). The tail characterizations there are associated with atypical bandit behavior on trajectories where the optimal arm mean is under-estimated, leading to mis-identification of the optimal arm and large regret. In contrast, our SLLN's and CLT's here describe the typical behavior and fluctuation of regret on trajectories where the optimal arm mean is properly estimated. We find that Thompson sampling and UCB satisfy the same SLLN and CLT, with the asymptotics of both the SLLN and the (mean) centering sequence in the CLT matching the asymptotics of expected regret. Both the mean and variance in the CLT grow at $\log(T)$ rates with the time horizon $T$. Asymptotically as $T \to \infty$, the variability in the number of plays of each sub-optimal arm depends only on the rewards received for that arm, which indicates that each sub-optimal arm contributes independently to the overall CLT variance.

The Fragility of Optimized Bandit Algorithms

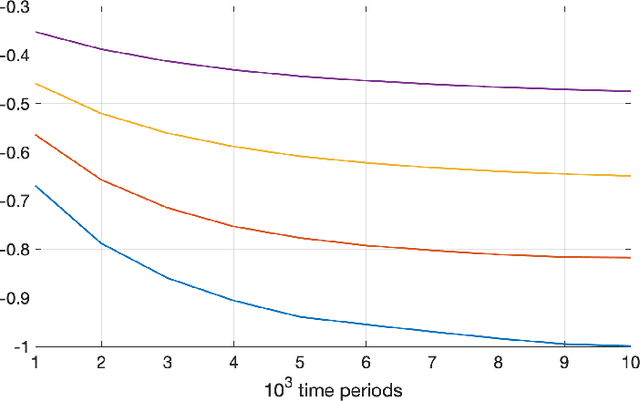
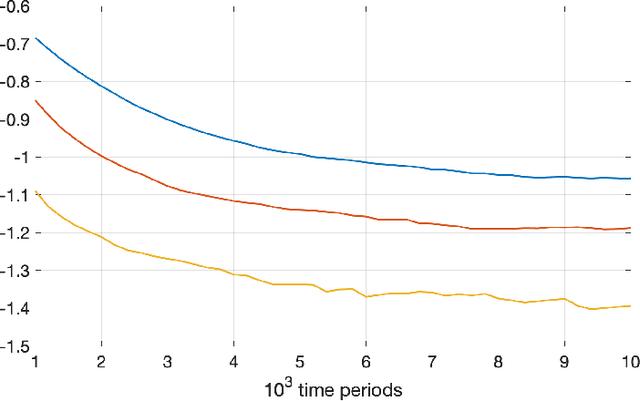
Much of the literature on optimal design of bandit algorithms is based on minimization of expected regret. It is well known that designs that are optimal over certain exponential families can achieve expected regret that grows logarithmically in the number of arm plays, at a rate governed by the Lai-Robbins lower bound. In this paper, we show that when one uses such optimized designs, the associated algorithms necessarily have the undesirable feature that the tail of the regret distribution behaves like that of a truncated Cauchy distribution. Furthermore, for $p>1$, the $p$'th moment of the regret distribution grows much faster than poly-logarithmically, in particular as a power of the number of sub-optimal arm plays. We show that optimized Thompson sampling and UCB bandit designs are also fragile, in the sense that when the problem is even slightly mis-specified, the regret can grow much faster than the conventional theory suggests. Our arguments are based on standard change-of-measure ideas, and indicate that the most likely way that regret becomes larger than expected is when the optimal arm returns below-average rewards in the first few arm plays that make that arm appear to be sub-optimal, thereby causing the algorithm to sample a truly sub-optimal arm much more than would be optimal.

Distributed stochastic optimization with large delays

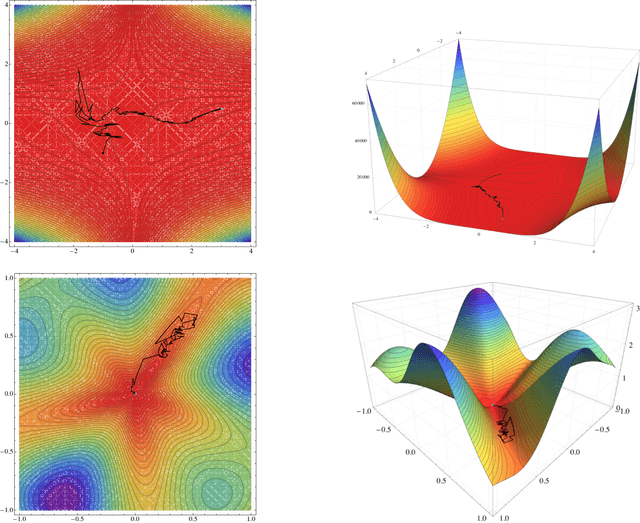
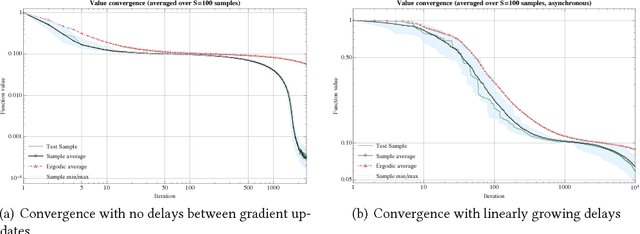
One of the most widely used methods for solving large-scale stochastic optimization problems is distributed asynchronous stochastic gradient descent (DASGD), a family of algorithms that result from parallelizing stochastic gradient descent on distributed computing architectures (possibly) asychronously. However, a key obstacle in the efficient implementation of DASGD is the issue of delays: when a computing node contributes a gradient update, the global model parameter may have already been updated by other nodes several times over, thereby rendering this gradient information stale. These delays can quickly add up if the computational throughput of a node is saturated, so the convergence of DASGD may be compromised in the presence of large delays. Our first contribution is that, by carefully tuning the algorithm's step-size, convergence to the critical set is still achieved in mean square, even if the delays grow unbounded at a polynomial rate. We also establish finer results in a broad class of structured optimization problems (called variationally coherent), where we show that DASGD converges to a global optimum with probability $1$ under the same delay assumptions. Together, these results contribute to the broad landscape of large-scale non-convex stochastic optimization by offering state-of-the-art theoretical guarantees and providing insights for algorithm design.

Diffusion Approximations for Thompson Sampling

We study the behavior of Thompson sampling from the perspective of weak convergence. In the regime where the gaps between arm means scale as $1/\sqrt{n}$ with the time horizon $n$, we show that the dynamics of Thompson sampling evolve according to discrete versions of SDEs and random ODEs. As $n \to \infty$, we show that the dynamics converge weakly to solutions of the corresponding SDEs and random ODEs. (Recently, Wager and Xu (arXiv:2101.09855) independently proposed this regime and developed similar SDE and random ODE approximations.) Our weak convergence theory covers both the classical multi-armed and linear bandit settings, and can be used, for instance, to obtain insight about the characteristics of the regret distribution when there is information sharing among arms, as well as the effects of variance estimation, model mis-specification and batched updates in bandit learning. Our theory is developed from first-principles and can also be adapted to analyze other sampling-based bandit algorithms.

On Incorporating Forecasts into Linear State Space Model Markov Decision Processes

Weather forecast information will very likely find increasing application in the control of future energy systems. In this paper, we introduce an augmented state space model formulation with linear dynamics, within which one can incorporate forecast information that is dynamically revealed alongside the evolution of the underlying state variable. We use the martingale model for forecast evolution (MMFE) to enforce the necessary consistency properties that must govern the joint evolution of forecasts with the underlying state. The formulation also generates jointly Markovian dynamics that give rise to Markov decision processes (MDPs) that remain computationally tractable. This paper is the first to enforce MMFE consistency requirements within an MDP formulation that preserves tractability.

Sequential Batch Learning in Finite-Action Linear Contextual Bandits

We study the sequential batch learning problem in linear contextual bandits with finite action sets, where the decision maker is constrained to split incoming individuals into (at most) a fixed number of batches and can only observe outcomes for the individuals within a batch at the batch's end. Compared to both standard online contextual bandits learning or offline policy learning in contexutal bandits, this sequential batch learning problem provides a finer-grained formulation of many personalized sequential decision making problems in practical applications, including medical treatment in clinical trials, product recommendation in e-commerce and adaptive experiment design in crowdsourcing. We study two settings of the problem: one where the contexts are arbitrarily generated and the other where the contexts are \textit{iid} drawn from some distribution. In each setting, we establish a regret lower bound and provide an algorithm, whose regret upper bound nearly matches the lower bound. As an important insight revealed therefrom, in the former setting, we show that the number of batches required to achieve the fully online performance is polynomial in the time horizon, while for the latter setting, a pure-exploitation algorithm with a judicious batch partition scheme achieves the fully online performance even when the number of batches is less than logarithmic in the time horizon. Together, our results provide a near-complete characterization of sequential decision making in linear contextual bandits when batch constraints are present.