Global Algorithms for Mean-Variance Optimization in Markov Decision Processes

Dynamic optimization of mean and variance in Markov decision processes (MDPs) is a long-standing challenge caused by the failure of dynamic programming. In this paper, we propose a new approach to find the globally optimal policy for combined metrics of steady-state mean and variance in an infinite-horizon undiscounted MDP. By introducing the concepts of pseudo mean and pseudo variance, we convert the original problem to a bilevel MDP problem, where the inner one is a standard MDP optimizing pseudo mean-variance and the outer one is a single parameter selection problem optimizing pseudo mean. We use the sensitivity analysis of MDPs to derive the properties of this bilevel problem. By solving inner standard MDPs for pseudo mean-variance optimization, we can identify worse policy spaces dominated by optimal policies of the pseudo problems. We propose an optimization algorithm which can find the globally optimal policy by repeatedly removing worse policy spaces. The convergence and complexity of the algorithm are studied. Another policy dominance property is also proposed to further improve the algorithm efficiency. Numerical experiments demonstrate the performance and efficiency of our algorithms. To the best of our knowledge, our algorithm is the first that efficiently finds the globally optimal policy of mean-variance optimization in MDPs. These results are also valid for solely minimizing the variance metrics in MDPs.

Risk-Sensitive Markov Decision Processes with Long-Run CVaR Criterion

CVaR (Conditional Value at Risk) is a risk metric widely used in finance. However, dynamically optimizing CVaR is difficult since it is not a standard Markov decision process (MDP) and the principle of dynamic programming fails. In this paper, we study the infinite-horizon discrete-time MDP with a long-run CVaR criterion, from the view of sensitivity-based optimization. By introducing a pseudo CVaR metric, we derive a CVaR difference formula which quantifies the difference of long-run CVaR under any two policies. The optimality of deterministic policies is derived. We obtain a so-called Bellman local optimality equation for CVaR, which is a necessary and sufficient condition for local optimal policies and only necessary for global optimal policies. A CVaR derivative formula is also derived for providing more sensitivity information. Then we develop a policy iteration type algorithm to efficiently optimize CVaR, which is shown to converge to local optima in the mixed policy space. We further discuss some extensions including the mean-CVaR optimization and the maximization of CVaR. Finally, we conduct numerical experiments relating to portfolio management to demonstrate the main results. Our work may shed light on dynamically optimizing CVaR from a sensitivity viewpoint.

Distributionally Robust Offline Reinforcement Learning with Linear Function Approximation

Among the reasons hindering reinforcement learning (RL) applications to real-world problems, two factors are critical: limited data and the mismatch between the testing environment (real environment in which the policy is deployed) and the training environment (e.g., a simulator). This paper attempts to address these issues simultaneously with distributionally robust offline RL, where we learn a distributionally robust policy using historical data obtained from the source environment by optimizing against a worst-case perturbation thereof. In particular, we move beyond tabular settings and consider linear function approximation. More specifically, we consider two settings, one where the dataset is well-explored and the other where the dataset has sufficient coverage. We propose two algorithms -- one for each of the two settings -- that achieve error bounds $\tilde{O}(d^{1/2}/N^{1/2})$ and $\tilde{O}(d^{3/2}/N^{1/2})$ respectively, where $d$ is the dimension in the linear function approximation and $N$ is the number of trajectories in the dataset. To the best of our knowledge, they provide the first non-asymptotic results of the sample complexity in this setting. Diverse experiments are conducted to demonstrate our theoretical findings, showing the superiority of our algorithm against the non-robust one.

Mean-Semivariance Policy Optimization via Risk-Averse Reinforcement Learning

Keeping risk under control is often more crucial than maximizing expected reward in real-world decision-making situations, such as finance, robotics, autonomous driving, etc. The most natural choice of risk measures is variance, while it penalizes the upside volatility as much as the downside part. Instead, the (downside) semivariance, which captures negative deviation of a random variable under its mean, is more suitable for risk-averse proposes. This paper aims at optimizing the mean-semivariance (MSV) criterion in reinforcement learning w.r.t. steady rewards. Since semivariance is time-inconsistent and does not satisfy the standard Bellman equation, the traditional dynamic programming methods are inapplicable to MSV problems directly. To tackle this challenge, we resort to the Perturbation Analysis (PA) theory and establish the performance difference formula for MSV. We reveal that the MSV problem can be solved by iteratively solving a sequence of RL problems with a policy-dependent reward function. Further, we propose two on-policy algorithms based on the policy gradient theory and the trust region method. Finally, we conduct diverse experiments from simple bandit problems to continuous control tasks in MuJoCo, which demonstrate the effectiveness of our proposed methods.

A unified algorithm framework for mean-variance optimization in discounted Markov decision processes

This paper studies the risk-averse mean-variance optimization in infinite-horizon discounted Markov decision processes (MDPs). The involved variance metric concerns reward variability during the whole process, and future deviations are discounted to their present values. This discounted mean-variance optimization yields a reward function dependent on a discounted mean, and this dependency renders traditional dynamic programming methods inapplicable since it suppresses a crucial property -- time consistency. To deal with this unorthodox problem, we introduce a pseudo mean to transform the untreatable MDP to a standard one with a redefined reward function in standard form and derive a discounted mean-variance performance difference formula. With the pseudo mean, we propose a unified algorithm framework with a bilevel optimization structure for the discounted mean-variance optimization. The framework unifies a variety of algorithms for several variance-related problems including, but not limited to, risk-averse variance and mean-variance optimizations in discounted and average MDPs. Furthermore, the convergence analyses missing from the literature can be complemented with the proposed framework as well. Taking the value iteration as an example, we develop a discounted mean-variance value iteration algorithm and prove its convergence to a local optimum with the aid of a Bellman local-optimality equation. Finally, we conduct a numerical experiment on portfolio management to validate the proposed algorithm.

Average-Reward Reinforcement Learning with Trust Region Methods

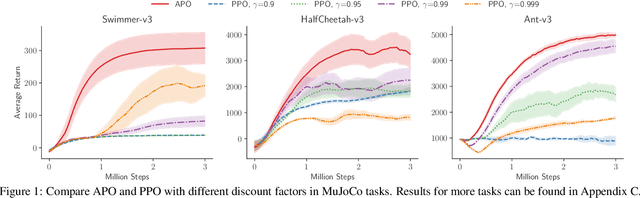
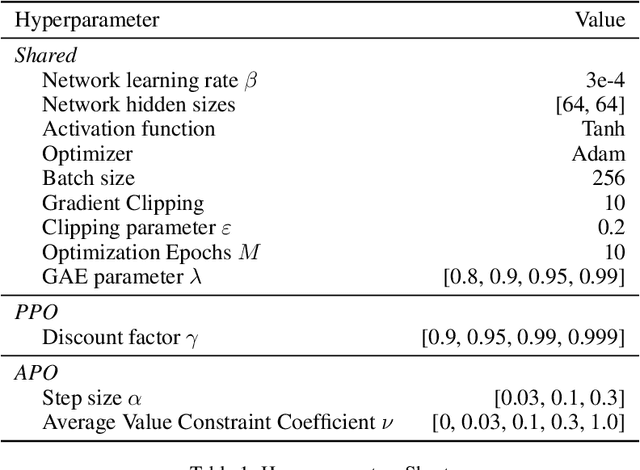
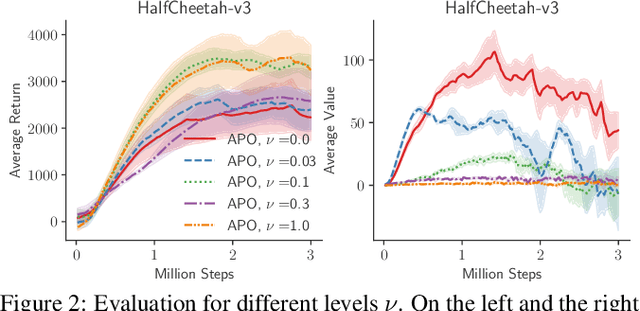
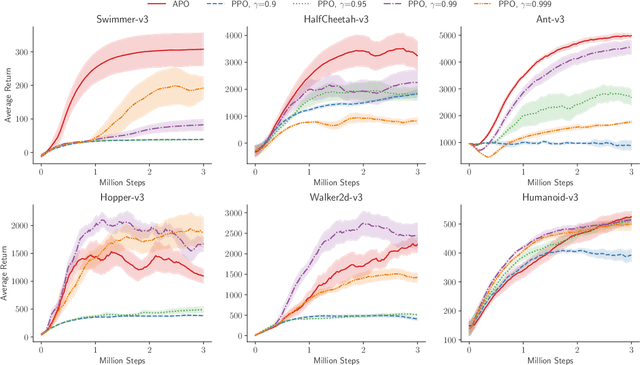
Most of reinforcement learning algorithms optimize the discounted criterion which is beneficial to accelerate the convergence and reduce the variance of estimates. Although the discounted criterion is appropriate for certain tasks such as financial related problems, many engineering problems treat future rewards equally and prefer a long-run average criterion. In this paper, we study the reinforcement learning problem with the long-run average criterion. Firstly, we develop a unified trust region theory with discounted and average criteria. With the average criterion, a novel performance bound within the trust region is derived with the Perturbation Analysis (PA) theory. Secondly, we propose a practical algorithm named Average Policy Optimization (APO), which improves the value estimation with a novel technique named Average Value Constraint. To the best of our knowledge, our work is the first one to study the trust region approach with the average criterion and it complements the framework of reinforcement learning beyond the discounted criterion. Finally, experiments are conducted in the continuous control environment MuJoCo. In most tasks, APO performs better than the discounted PPO, which demonstrates the effectiveness of our approach.

Risk-Sensitive Markov Decision Processes with Combined Metrics of Mean and Variance

This paper investigates the optimization problem of an infinite stage discrete time Markov decision process (MDP) with a long-run average metric considering both mean and variance of rewards together. Such performance metric is important since the mean indicates average returns and the variance indicates risk or fairness. However, the variance metric couples the rewards at all stages, the traditional dynamic programming is inapplicable as the principle of time consistency fails. We study this problem from a new perspective called the sensitivity-based optimization theory. A performance difference formula is derived and it can quantify the difference of the mean-variance combined metrics of MDPs under any two different policies. The difference formula can be utilized to generate new policies with strictly improved mean-variance performance. A necessary condition of the optimal policy and the optimality of deterministic policies are derived. We further develop an iterative algorithm with a form of policy iteration, which is proved to converge to local optima both in the mixed and randomized policy space. Specially, when the mean reward is constant in policies, the algorithm is guaranteed to converge to the global optimum. Finally, we apply our approach to study the fluctuation reduction of wind power in an energy storage system, which demonstrates the potential applicability of our optimization method.

Embedding-based Retrieval in Facebook Search

Search in social networks such as Facebook poses different challenges than in classical web search: besides the query text, it is important to take into account the searcher's context to provide relevant results. Their social graph is an integral part of this context and is a unique aspect of Facebook search. While embedding-based retrieval (EBR) has been applied in eb search engines for years, Facebook search was still mainly based on a Boolean matching model. In this paper, we discuss the techniques for applying EBR to a Facebook Search system. We introduce the unified embedding framework developed to model semantic embeddings for personalized search, and the system to serve embedding-based retrieval in a typical search system based on an inverted index. We discuss various tricks and experiences on end-to-end optimization of the whole system, including ANN parameter tuning and full-stack optimization. Finally, we present our progress on two selected advanced topics about modeling. We evaluated EBR on verticals for Facebook Search with significant metrics gains observed in online A/B experiments. We believe this paper will provide useful insights and experiences to help people on developing embedding-based retrieval systems in search engines.

SOAC: The Soft Option Actor-Critic Architecture

The option framework has shown great promise by automatically extracting temporally-extended sub-tasks from a long-horizon task. Methods have been proposed for concurrently learning low-level intra-option policies and high-level option selection policy. However, existing methods typically suffer from two major challenges: ineffective exploration and unstable updates. In this paper, we present a novel and stable off-policy approach that builds on the maximum entropy model to address these challenges. Our approach introduces an information-theoretical intrinsic reward for encouraging the identification of diverse and effective options. Meanwhile, we utilize a probability inference model to simplify the optimization problem as fitting optimal trajectories. Experimental results demonstrate that our approach significantly outperforms prior on-policy and off-policy methods in a range of Mujoco benchmark tasks while still providing benefits for transfer learning. In these tasks, our approach learns a diverse set of options, each of whose state-action space has strong coherence.