Step-CoT: Stepwise Visual Chain-of-Thought for Medical Visual Question Answering

Chain-of-thought (CoT) reasoning has advanced medical visual question answering (VQA), yet most existing CoT rationales are free-form and fail to capture the structured reasoning process clinicians actually follow. This work asks: Can traceable, multi-step reasoning supervision improve reasoning accuracy and the interpretability of Medical VQA? To this end, we introduce Step-CoT, a large-scale medical reasoning dataset with expert-curated, structured multi-step CoT aligned to clinical diagnostic workflows, implicitly grounding the model's reasoning in radiographic evidence. Step-CoT comprises more than 10K real clinical cases and 70K VQA pairs organized around diagnostic workflows, providing supervised intermediate steps that guide models to follow valid reasoning trajectories. To effectively learn from Step-CoT, we further introduce a teacher-student framework with a dynamic graph-structured focusing mechanism that prioritizes diagnostically informative steps while filtering out less relevant contexts. Our experiments show that using Step-CoT can improve reasoning accuracy and interpretability. Benchmark: github.com/hahaha111111/Step-CoT. Dataset Card: huggingface.co/datasets/fl-15o/Step-CoT

RAVEL: Reasoning Agents for Validating and Evaluating LLM Text Synthesis

Large Language Models have evolved from single-round generators into long-horizon agents, capable of complex text synthesis scenarios. However, current evaluation frameworks lack the ability to assess the actual synthesis operations, such as outlining, drafting, and editing. Consequently, they fail to evaluate the actual and detailed capabilities of LLMs. To bridge this gap, we introduce RAVEL, an agentic framework that enables the LLM testers to autonomously plan and execute typical synthesis operations, including outlining, drafting, reviewing, and refining. Complementing this framework, we present C3EBench, a comprehensive benchmark comprising 1,258 samples derived from professional human writings. We utilize a "reverse-engineering" pipeline to isolate specific capabilities across four tasks: Cloze, Edit, Expand, and End-to-End. Through our analysis of 14 LLMs, we uncover that most LLMs struggle with tasks that demand contextual understanding under limited or under-specified instructions. By augmenting RAVEL with SOTA LLMs as operators, we find that such agentic text synthesis is dominated by the LLM's reasoning capability rather than raw generative capacity. Furthermore, we find that a strong reasoner can guide a weaker generator to yield higher-quality results, whereas the inverse does not hold. Our code and data are available at this link: https://github.com/ZhuoerFeng/RAVEL-Reasoning-Agents-Text-Eval.

GLM-5: from Vibe Coding to Agentic Engineering

We present GLM-5, a next-generation foundation model designed to transition the paradigm of vibe coding to agentic engineering. Building upon the agentic, reasoning, and coding (ARC) capabilities of its predecessor, GLM-5 adopts DSA to significantly reduce training and inference costs while maintaining long-context fidelity. To advance model alignment and autonomy, we implement a new asynchronous reinforcement learning infrastructure that drastically improves post-training efficiency by decoupling generation from training. Furthermore, we propose novel asynchronous agent RL algorithms that further improve RL quality, enabling the model to learn from complex, long-horizon interactions more effectively. Through these innovations, GLM-5 achieves state-of-the-art performance on major open benchmarks. Most critically, GLM-5 demonstrates unprecedented capability in real-world coding tasks, surpassing previous baselines in handling end-to-end software engineering challenges. Code, models, and more information are available at https://github.com/zai-org/GLM-5.

GLM-4.5: Agentic, Reasoning, and Coding (ARC) Foundation Models

We present GLM-4.5, an open-source Mixture-of-Experts (MoE) large language model with 355B total parameters and 32B activated parameters, featuring a hybrid reasoning method that supports both thinking and direct response modes. Through multi-stage training on 23T tokens and comprehensive post-training with expert model iteration and reinforcement learning, GLM-4.5 achieves strong performance across agentic, reasoning, and coding (ARC) tasks, scoring 70.1% on TAU-Bench, 91.0% on AIME 24, and 64.2% on SWE-bench Verified. With much fewer parameters than several competitors, GLM-4.5 ranks 3rd overall among all evaluated models and 2nd on agentic benchmarks. We release both GLM-4.5 (355B parameters) and a compact version, GLM-4.5-Air (106B parameters), to advance research in reasoning and agentic AI systems. Code, models, and more information are available at https://github.com/zai-org/GLM-4.5.

Tri-VQA: Triangular Reasoning Medical Visual Question Answering for Multi-Attribute Analysis

The intersection of medical Visual Question Answering (Med-VQA) is a challenging research topic with advantages including patient engagement and clinical expert involvement for second opinions. However, existing Med-VQA methods based on joint embedding fail to explain whether their provided results are based on correct reasoning or coincidental answers, which undermines the credibility of VQA answers. In this paper, we investigate the construction of a more cohesive and stable Med-VQA structure. Motivated by causal effect, we propose a novel Triangular Reasoning VQA (Tri-VQA) framework, which constructs reverse causal questions from the perspective of "Why this answer?" to elucidate the source of the answer and stimulate more reasonable forward reasoning processes. We evaluate our method on the Endoscopic Ultrasound (EUS) multi-attribute annotated dataset from five centers, and test it on medical VQA datasets. Experimental results demonstrate the superiority of our approach over existing methods. Our codes and pre-trained models are available at https://anonymous.4open.science/r/Tri_VQA.

MDA: An Interpretable Multi-Modal Fusion with Missing Modalities and Intrinsic Noise

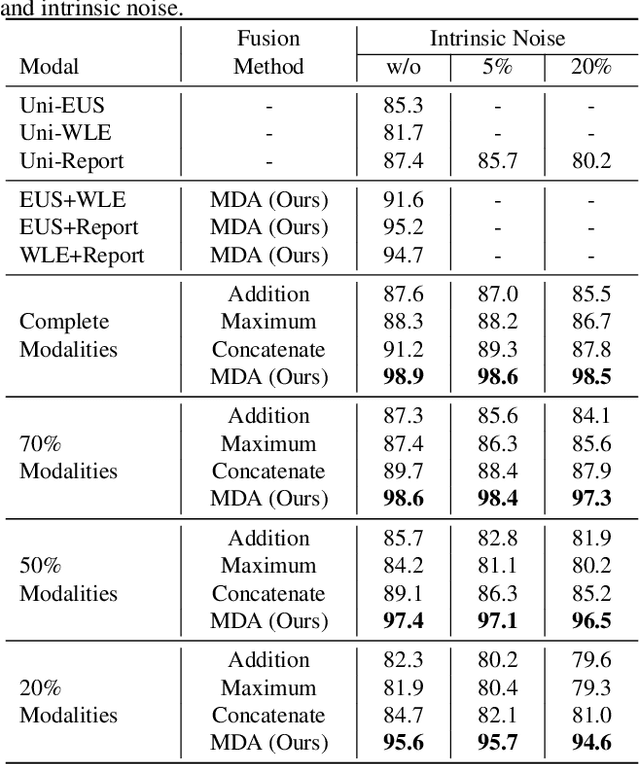
Multi-modal fusion is crucial in medical data research, enabling a comprehensive understanding of diseases and improving diagnostic performance by combining diverse modalities. However, multi-modal fusion faces challenges, including capturing interactions between modalities, addressing missing modalities, handling erroneous modal information, and ensuring interpretability. Many existing researchers tend to design different solutions for these problems, often overlooking the commonalities among them. This paper proposes a novel multi-modal fusion framework that achieves adaptive adjustment over the weights of each modality by introducing the Modal-Domain Attention (MDA). It aims to facilitate the fusion of multi-modal information while allowing for the inclusion of missing modalities or intrinsic noise, thereby enhancing the representation of multi-modal data. We provide visualizations of accuracy changes and MDA weights by observing the process of modal fusion, offering a comprehensive analysis of its interpretability. Extensive experiments on various gastrointestinal disease benchmarks, the proposed MDA maintains high accuracy even in the presence of missing modalities and intrinsic noise. One thing worth mentioning is that the visualization of MDA is highly consistent with the conclusions of existing clinical studies on the dependence of different diseases on various modalities. Code and dataset will be made available.

The Typical Behavior of Bandit Algorithms

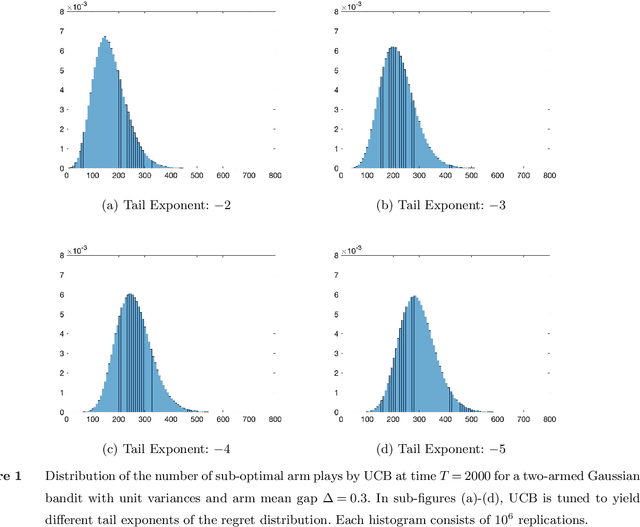
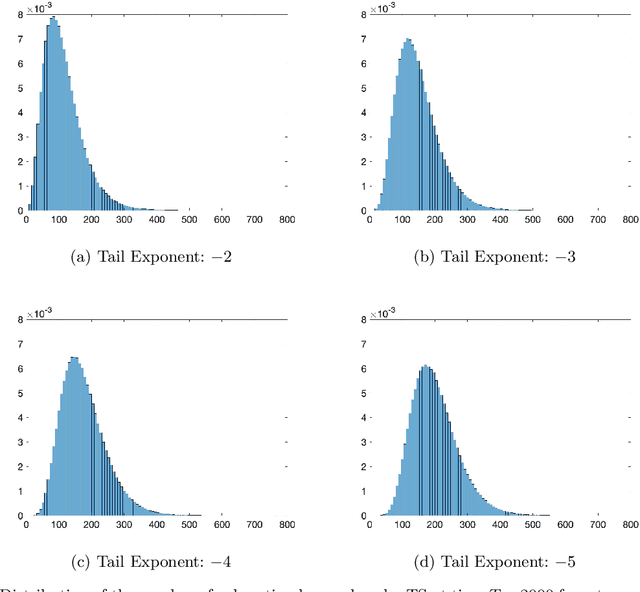
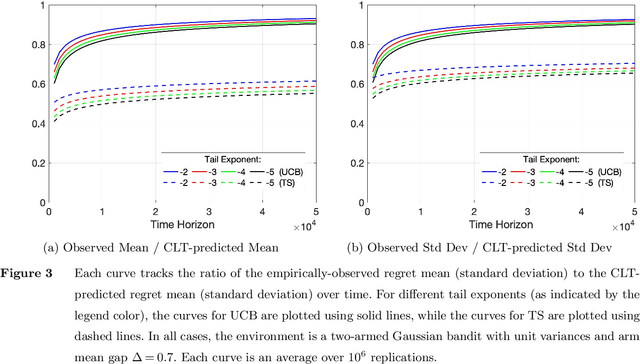
We establish strong laws of large numbers and central limit theorems for the regret of two of the most popular bandit algorithms: Thompson sampling and UCB. Here, our characterizations of the regret distribution complement the characterizations of the tail of the regret distribution recently developed by Fan and Glynn (2021) (arXiv:2109.13595). The tail characterizations there are associated with atypical bandit behavior on trajectories where the optimal arm mean is under-estimated, leading to mis-identification of the optimal arm and large regret. In contrast, our SLLN's and CLT's here describe the typical behavior and fluctuation of regret on trajectories where the optimal arm mean is properly estimated. We find that Thompson sampling and UCB satisfy the same SLLN and CLT, with the asymptotics of both the SLLN and the (mean) centering sequence in the CLT matching the asymptotics of expected regret. Both the mean and variance in the CLT grow at $\log(T)$ rates with the time horizon $T$. Asymptotically as $T \to \infty$, the variability in the number of plays of each sub-optimal arm depends only on the rewards received for that arm, which indicates that each sub-optimal arm contributes independently to the overall CLT variance.

The Fragility of Optimized Bandit Algorithms

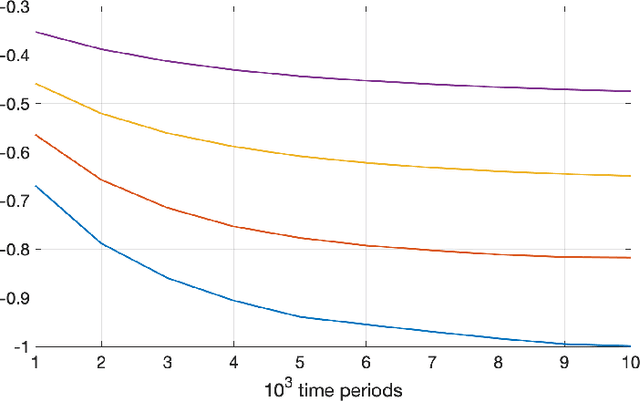
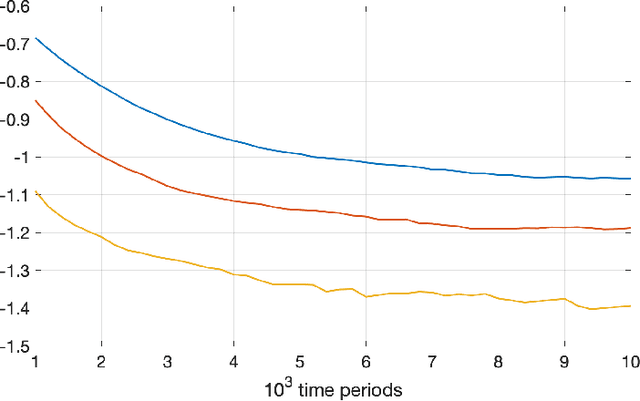
Much of the literature on optimal design of bandit algorithms is based on minimization of expected regret. It is well known that designs that are optimal over certain exponential families can achieve expected regret that grows logarithmically in the number of arm plays, at a rate governed by the Lai-Robbins lower bound. In this paper, we show that when one uses such optimized designs, the associated algorithms necessarily have the undesirable feature that the tail of the regret distribution behaves like that of a truncated Cauchy distribution. Furthermore, for $p>1$, the $p$'th moment of the regret distribution grows much faster than poly-logarithmically, in particular as a power of the number of sub-optimal arm plays. We show that optimized Thompson sampling and UCB bandit designs are also fragile, in the sense that when the problem is even slightly mis-specified, the regret can grow much faster than the conventional theory suggests. Our arguments are based on standard change-of-measure ideas, and indicate that the most likely way that regret becomes larger than expected is when the optimal arm returns below-average rewards in the first few arm plays that make that arm appear to be sub-optimal, thereby causing the algorithm to sample a truly sub-optimal arm much more than would be optimal.

Diffusion Approximations for Thompson Sampling

We study the behavior of Thompson sampling from the perspective of weak convergence. In the regime where the gaps between arm means scale as $1/\sqrt{n}$ with the time horizon $n$, we show that the dynamics of Thompson sampling evolve according to discrete versions of SDEs and random ODEs. As $n \to \infty$, we show that the dynamics converge weakly to solutions of the corresponding SDEs and random ODEs. (Recently, Wager and Xu (arXiv:2101.09855) independently proposed this regime and developed similar SDE and random ODE approximations.) Our weak convergence theory covers both the classical multi-armed and linear bandit settings, and can be used, for instance, to obtain insight about the characteristics of the regret distribution when there is information sharing among arms, as well as the effects of variance estimation, model mis-specification and batched updates in bandit learning. Our theory is developed from first-principles and can also be adapted to analyze other sampling-based bandit algorithms.