The Fragility of Optimized Bandit Algorithms
Paper and Code
Sep 28, 2021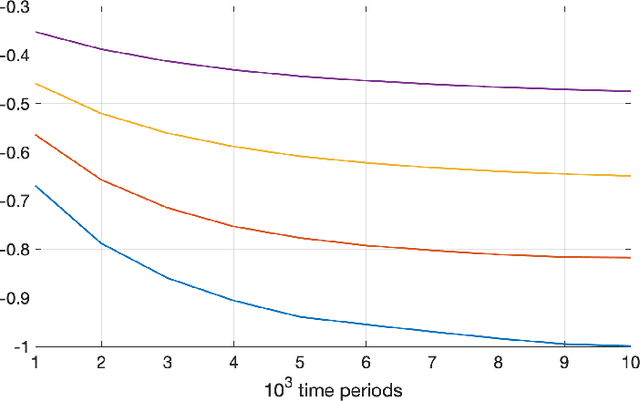
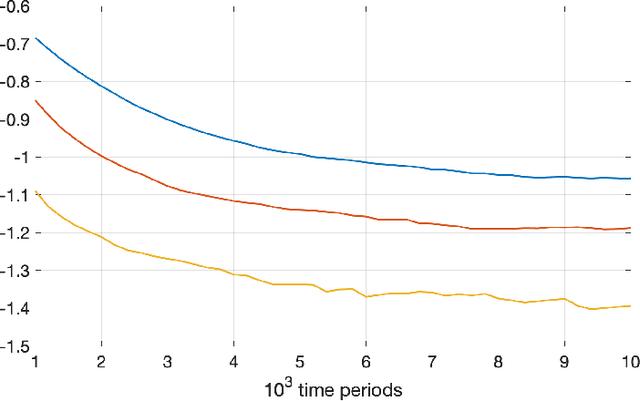
Much of the literature on optimal design of bandit algorithms is based on minimization of expected regret. It is well known that designs that are optimal over certain exponential families can achieve expected regret that grows logarithmically in the number of arm plays, at a rate governed by the Lai-Robbins lower bound. In this paper, we show that when one uses such optimized designs, the associated algorithms necessarily have the undesirable feature that the tail of the regret distribution behaves like that of a truncated Cauchy distribution. Furthermore, for $p>1$, the $p$'th moment of the regret distribution grows much faster than poly-logarithmically, in particular as a power of the number of sub-optimal arm plays. We show that optimized Thompson sampling and UCB bandit designs are also fragile, in the sense that when the problem is even slightly mis-specified, the regret can grow much faster than the conventional theory suggests. Our arguments are based on standard change-of-measure ideas, and indicate that the most likely way that regret becomes larger than expected is when the optimal arm returns below-average rewards in the first few arm plays that make that arm appear to be sub-optimal, thereby causing the algorithm to sample a truly sub-optimal arm much more than would be optimal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge