Calibrating Over-Parametrized Simulation Models: A Framework via Eligibility Set
Paper and Code
May 27, 2021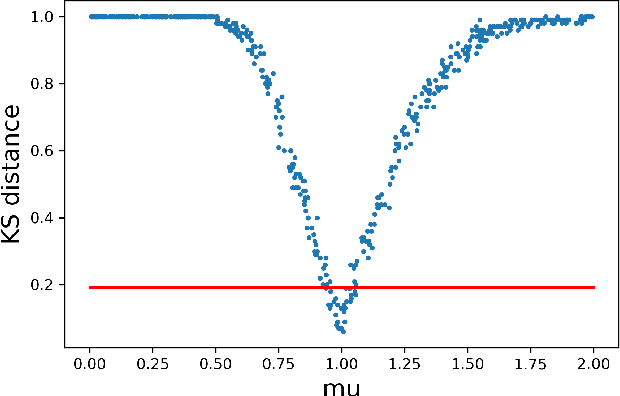

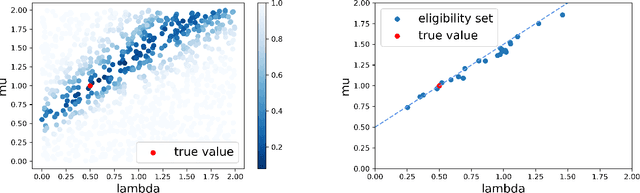
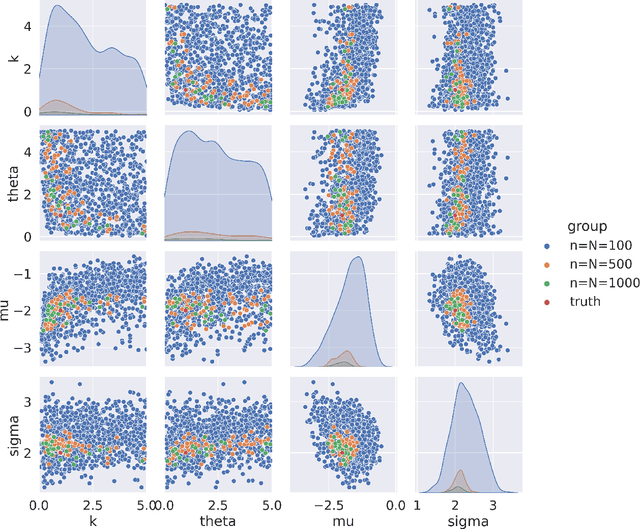
Stochastic simulation aims to compute output performance for complex models that lack analytical tractability. To ensure accurate prediction, the model needs to be calibrated and validated against real data. Conventional methods approach these tasks by assessing the model-data match via simple hypothesis tests or distance minimization in an ad hoc fashion, but they can encounter challenges arising from non-identifiability and high dimensionality. In this paper, we investigate a framework to develop calibration schemes that satisfy rigorous frequentist statistical guarantees, via a basic notion that we call eligibility set designed to bypass non-identifiability via a set-based estimation. We investigate a feature extraction-then-aggregation approach to construct these sets that target at multivariate outputs. We demonstrate our methodology on several numerical examples, including an application to calibration of a limit order book market simulator (ABIDES).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge