LLM Embeddings Improve Test-time Adaptation to Tabular $Y|X$-Shifts

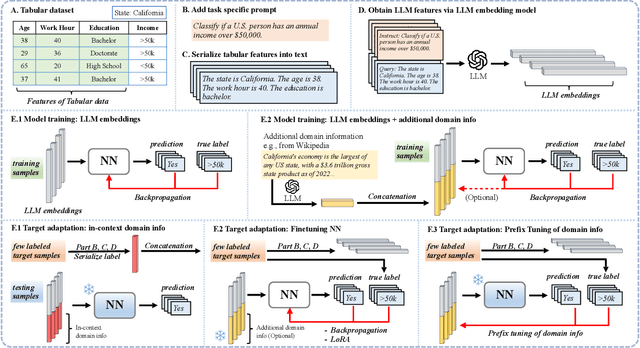
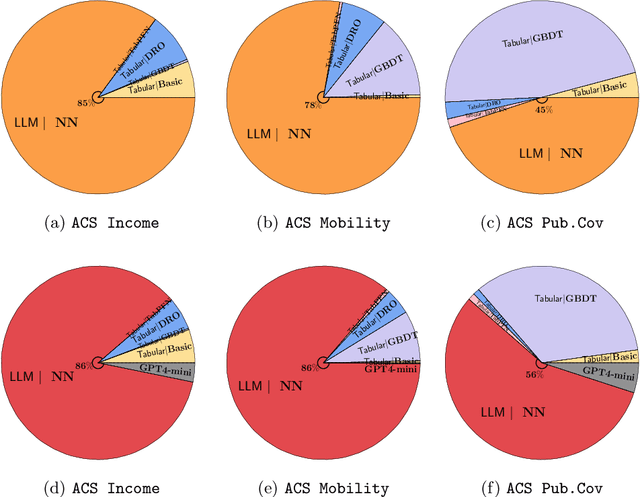
For tabular datasets, the change in the relationship between the label and covariates ($Y|X$-shifts) is common due to missing variables (a.k.a. confounders). Since it is impossible to generalize to a completely new and unknown domain, we study models that are easy to adapt to the target domain even with few labeled examples. We focus on building more informative representations of tabular data that can mitigate $Y|X$-shifts, and propose to leverage the prior world knowledge in LLMs by serializing (write down) the tabular data to encode it. We find LLM embeddings alone provide inconsistent improvements in robustness, but models trained on them can be well adapted/finetuned to the target domain even using 32 labeled observations. Our finding is based on a comprehensive and systematic study consisting of 7650 source-target pairs and benchmark against 261,000 model configurations trained by 22 algorithms. Our observation holds when ablating the size of accessible target data and different adaptation strategies. The code is available at https://github.com/namkoong-lab/LLM-Tabular-Shifts.

Design and Scheduling of an AI-based Queueing System

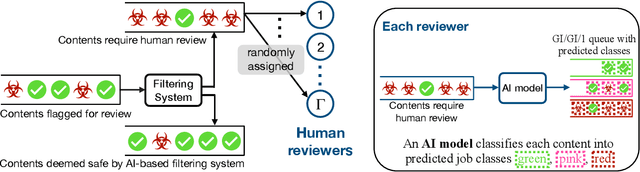
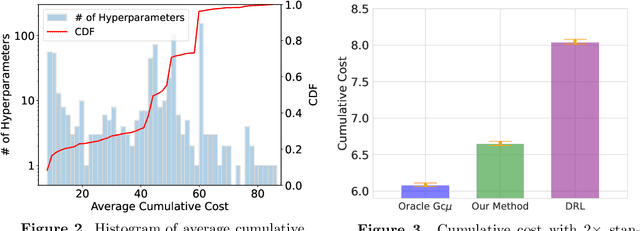
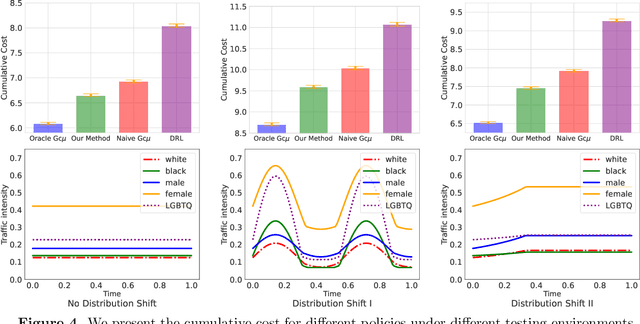
To leverage prediction models to make optimal scheduling decisions in service systems, we must understand how predictive errors impact congestion due to externalities on the delay of other jobs. Motivated by applications where prediction models interact with human servers (e.g., content moderation), we consider a large queueing system comprising of many single server queues where the class of a job is estimated using a prediction model. By characterizing the impact of mispredictions on congestion cost in heavy traffic, we design an index-based policy that incorporates the predicted class information in a near-optimal manner. Our theoretical results guide the design of predictive models by providing a simple model selection procedure with downstream queueing performance as a central concern, and offer novel insights on how to design queueing systems with AI-based triage. We illustrate our framework on a content moderation task based on real online comments, where we construct toxicity classifiers by finetuning large language models.

Complexity-Free Generalization via Distributionally Robust Optimization

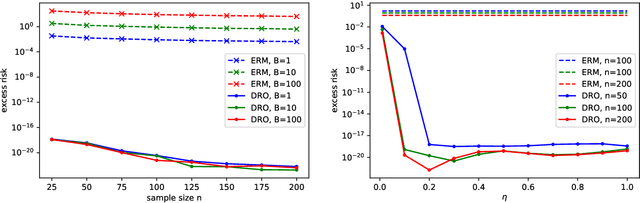
Established approaches to obtain generalization bounds in data-driven optimization and machine learning mostly build on solutions from empirical risk minimization (ERM), which depend crucially on the functional complexity of the hypothesis class. In this paper, we present an alternate route to obtain these bounds on the solution from distributionally robust optimization (DRO), a recent data-driven optimization framework based on worst-case analysis and the notion of ambiguity set to capture statistical uncertainty. In contrast to the hypothesis class complexity in ERM, our DRO bounds depend on the ambiguity set geometry and its compatibility with the true loss function. Notably, when using maximum mean discrepancy as a DRO distance metric, our analysis implies, to the best of our knowledge, the first generalization bound in the literature that depends solely on the true loss function, entirely free of any complexity measures or bounds on the hypothesis class.

AsyncQVI: Asynchronous-Parallel Q-Value Iteration for Reinforcement Learning with Near-Optimal Sample Complexity

In this paper, we propose AsyncQVI: Asynchronous-Parallel Q-value Iteration to solve Reinforcement Learning (RL) problems. Given an RL problem with $|\mathcal{S}|$ states, $|\mathcal{A}|$ actions, and a discounted factor $\gamma\in(0,1)$, AsyncQVI returns an $\varepsilon$-optimal policy with probability at least $1-\delta$ at the sample complexity $$\tilde{\mathcal{O}}\bigg(\frac{|\mathcal{S}||\mathcal{A}|}{(1-\gamma)^5\varepsilon^2}\log\Big(\frac{1}{\delta}\Big)\bigg).$$ AsyncQVI is the first asynchronous-parallel RL algorithm with convergence rate analysis and an explicit sample complexity. The above sample complexity of AsyncQVI nearly matches the lower bound. Furthermore, AsyncQVI is scalable since it has low memory footprint at $\mathcal{O}(|\mathcal{S}|)$ and also has an efficient asynchronous-parallel implementation.