Smoothed $f$-Divergence Distributionally Robust Optimization: Exponential Rate Efficiency and Complexity-Free Calibration

In data-driven optimization, sample average approximation is known to suffer from the so-called optimizer's curse that causes optimistic bias in evaluating the solution performance. This can be tackled by adding a "margin" to the estimated objective value, or via distributionally robust optimization (DRO), a fast-growing approach based on worst-case analysis, which gives a protective bound on the attained objective value. However, in all these existing approaches, a statistically guaranteed bound on the true solution performance either requires restrictive conditions and knowledge on the objective function complexity, or otherwise exhibits an over-conservative rate that depends on the distribution dimension. We argue that a special type of DRO offers strong theoretical advantages in regard to these challenges: It attains a statistical bound on the true solution performance that is the tightest possible in terms of exponential decay rate, for a wide class of objective functions that notably does not hinge on function complexity. Correspondingly, its calibration also does not require any complexity information. This DRO uses an ambiguity set based on a KL-divergence smoothed by the Wasserstein or Levy-Prokhorov distance via a suitable distance optimization. Computationally, we also show that such a DRO, and its generalized version using smoothed $f$-divergence, is not much harder than standard DRO problems using the $f$-divergence or Wasserstein distance, thus supporting the strengths of such DRO as both statistically optimal and computationally viable.

Learning and Decision-Making with Data: Optimal Formulations and Phase Transitions

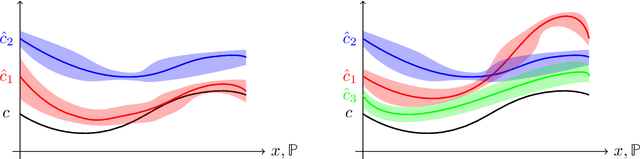
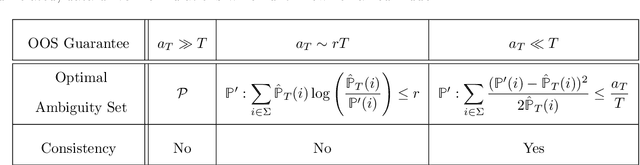
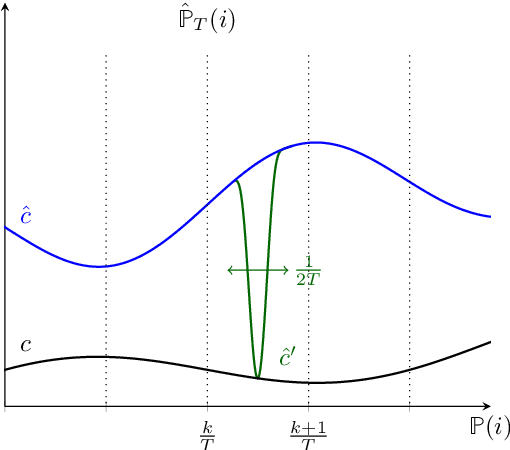
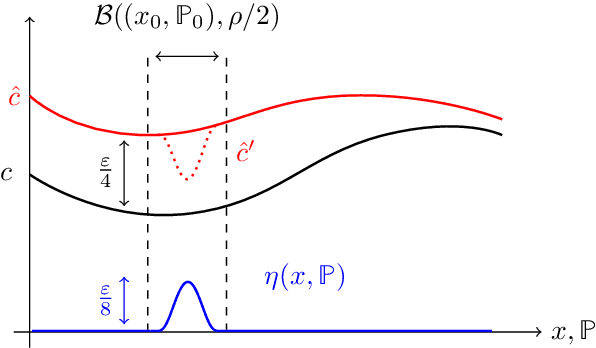
We study the problem of designing optimal learning and decision-making formulations when only historical data is available. Prior work typically commits to a particular class of data-driven formulation and subsequently tries to establish out-of-sample performance guarantees. We take here the opposite approach. We define first a sensible yard stick with which to measure the quality of any data-driven formulation and subsequently seek to find an optimal such formulation. Informally, any data-driven formulation can be seen to balance a measure of proximity of the estimated cost to the actual cost while guaranteeing a level of out-of-sample performance. Given an acceptable level of out-of-sample performance, we construct explicitly a data-driven formulation that is uniformly closer to the true cost than any other formulation enjoying the same out-of-sample performance. We show the existence of three distinct out-of-sample performance regimes (a superexponential regime, an exponential regime and a subexponential regime) between which the nature of the optimal data-driven formulation experiences a phase transition. The optimal data-driven formulations can be interpreted as a classically robust formulation in the superexponential regime, an entropic distributionally robust formulation in the exponential regime and finally a variance penalized formulation in the subexponential regime. This final observation unveils a surprising connection between these three, at first glance seemingly unrelated, data-driven formulations which until now remained hidden.

Optimal Transport in the Face of Noisy Data

Optimal transport distances are popular and theoretically well understood in the context of data-driven prediction. A flurry of recent work has popularized these distances for data-driven decision-making as well although their merits in this context are far less well understood. This in contrast to the more classical entropic distances which are known to enjoy optimal statistical properties. This begs the question when, if ever, optimal transport distances enjoy similar statistical guarantees. Optimal transport methods are shown here to enjoy optimal statistical guarantees for decision problems faced with noisy data.

Optimal Learning for Structured Bandits

We study structured multi-armed bandits, which is the problem of online decision-making under uncertainty in the presence of structural information. In this problem, the decision-maker needs to discover the best course of action despite observing only uncertain rewards over time. The decision-maker is aware of certain structural information regarding the reward distributions and would like to minimize his regret by exploiting this information, where the regret is its performance difference against a benchmark policy which knows the best action ahead of time. In the absence of structural information, the classical UCB and Thomson sampling algorithms are well known to suffer only minimal regret. As recently pointed out, neither algorithms is, however, capable of exploiting structural information which is commonly available in practice. We propose a novel learning algorithm which we call "DUSA" whose worst-case regret matches the information-theoretic regret lower bound up to a constant factor and can handle a wide range of structural information. Our algorithm DUSA solves a dual counterpart of regret lower bound at the empirical reward distribution and follows the suggestion made by the dual problem. Our proposed algorithm is the first computationally viable learning policy for structured bandit problems that suffers asymptotic minimal regret.