A Doubly Robust Approach to Sparse Reinforcement Learning

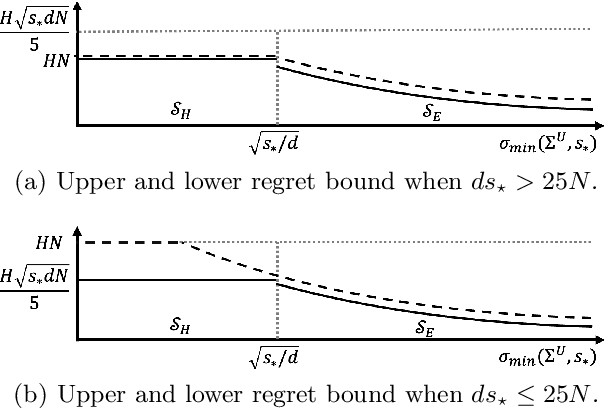
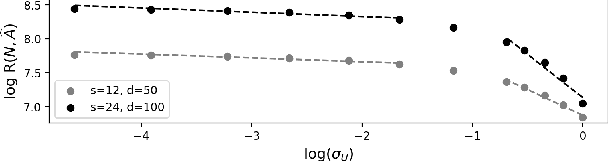
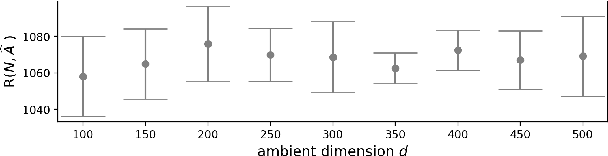
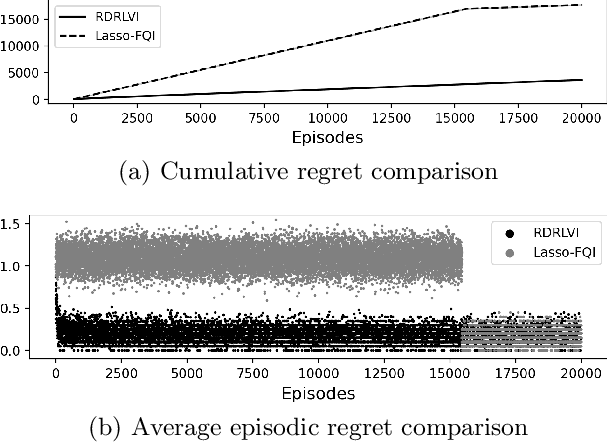
We propose a new regret minimization algorithm for episodic sparse linear Markov decision process (SMDP) where the state-transition distribution is a linear function of observed features. The only previously known algorithm for SMDP requires the knowledge of the sparsity parameter and oracle access to an unknown policy. We overcome these limitations by combining the doubly robust method that allows one to use feature vectors of \emph{all} actions with a novel analysis technique that enables the algorithm to use data from all periods in all episodes. The regret of the proposed algorithm is $\tilde{O}(\sigma^{-1}_{\min} s_{\star} H \sqrt{N})$, where $\sigma_{\min}$ denotes the restrictive the minimum eigenvalue of the average Gram matrix of feature vectors, $s_\star$ is the sparsity parameter, $H$ is the length of an episode, and $N$ is the number of rounds. We provide a lower regret bound that matches the upper bound up to logarithmic factors on a newly identified subclass of SMDPs. Our numerical experiments support our theoretical results and demonstrate the superior performance of our algorithm.

Bayesian Design Principles for Frequentist Sequential Learning

We develop a general theory to optimize the frequentist regret for sequential learning problems, where efficient bandit and reinforcement learning algorithms can be derived from unified Bayesian principles. We propose a novel optimization approach to generate "algorithmic beliefs" at each round, and use Bayesian posteriors to make decisions. The optimization objective to create "algorithmic beliefs," which we term "Algorithmic Information Ratio," represents an intrinsic complexity measure that effectively characterizes the frequentist regret of any algorithm. To the best of our knowledge, this is the first systematical approach to make Bayesian-type algorithms prior-free and applicable to adversarial settings, in a generic and optimal manner. Moreover, the algorithms are simple and often efficient to implement. As a major application, we present a novel algorithm for multi-armed bandits that achieves the "best-of-all-worlds" empirical performance in the stochastic, adversarial, and non-stationary environments. And we illustrate how these principles can be used in linear bandits, bandit convex optimization, and reinforcement learning.

Last Switch Dependent Bandits with Monotone Payoff Functions

In a recent work, Laforgue et al. introduce the model of last switch dependent (LSD) bandits, in an attempt to capture nonstationary phenomena induced by the interaction between the player and the environment. Examples include satiation, where consecutive plays of the same action lead to decreased performance, or deprivation, where the payoff of an action increases after an interval of inactivity. In this work, we take a step towards understanding the approximability of planning LSD bandits, namely, the (NP-hard) problem of computing an optimal arm-pulling strategy under complete knowledge of the model. In particular, we design the first efficient constant approximation algorithm for the problem and show that, under a natural monotonicity assumption on the payoffs, its approximation guarantee (almost) matches the state-of-the-art for the special and well-studied class of recharging bandits (also known as delay-dependent). In this attempt, we develop new tools and insights for this class of problems, including a novel higher-dimensional relaxation and the technique of mirroring the evolution of virtual states. We believe that these novel elements could potentially be used for approaching richer classes of action-induced nonstationary bandits (e.g., special instances of restless bandits). In the case where the model parameters are initially unknown, we develop an online learning adaptation of our algorithm for which we provide sublinear regret guarantees against its full-information counterpart.

Pareto Front Identification with Regret Minimization

We consider Pareto front identification for linear bandits (PFILin) where the goal is to identify a set of arms whose reward vectors are not dominated by any of the others when the mean reward vector is a linear function of the context. PFILin includes the best arm identification problem and multi-objective active learning as special cases. The sample complexity of our proposed algorithm is $\tilde{O}(d/\Delta^2)$, where $d$ is the dimension of contexts and $\Delta$ is a measure of problem complexity. Our sample complexity is optimal up to a logarithmic factor. A novel feature of our algorithm is that it uses the contexts of all actions. In addition to efficiently identifying the Pareto front, our algorithm also guarantees $\tilde{O}(\sqrt{d/t})$ bound for instantaneous Pareto regret when the number of samples is larger than $\Omega(d\log dL)$ for $L$ dimensional vector rewards. By using the contexts of all arms, our proposed algorithm simultaneously provides efficient Pareto front identification and regret minimization. Numerical experiments demonstrate that the proposed algorithm successfully identifies the Pareto front while minimizing the regret.

Improved Algorithms for Multi-period Multi-class Packing Problems with~Bandit~Feedback

We consider the linear contextual multi-class multi-period packing problem~(LMMP) where the goal is to pack items such that the total vector of consumption is below a given budget vector and the total value is as large as possible. We consider the setting where the reward and the consumption vector associated with each action is a class-dependent linear function of the context, and the decision-maker receives bandit feedback. LMMP includes linear contextual bandits with knapsacks and online revenue management as special cases. We establish a new more efficient estimator which guarantees a faster convergence rate, and consequently, a lower regret in such problems. We propose a bandit policy that is a closed-form function of said estimated parameters. When the contexts are non-degenerate, the regret of the proposed policy is sublinear in the context dimension, the number of classes, and the time horizon~$T$ when the budget grows at least as $\sqrt{T}$. We also resolve an open problem posed in Agrawal & Devanur (2016), and extend the result to a multi-class setting. Our numerical experiments clearly demonstrate that the performance of our policy is superior to other benchmarks in the literature.

Complexity Analysis of a Countable-armed Bandit Problem

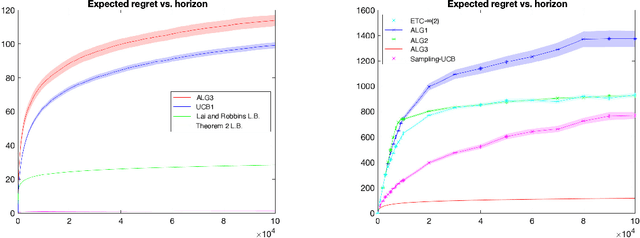
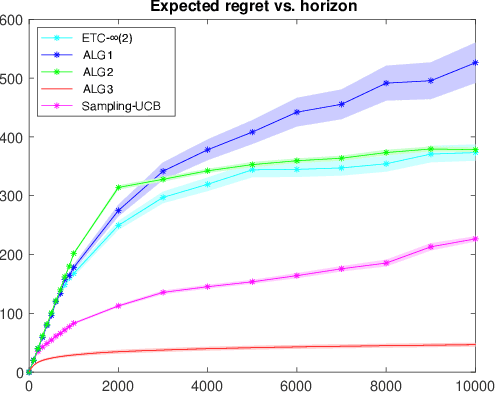
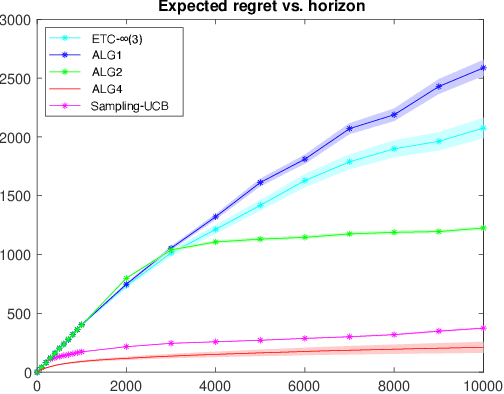
We consider a stochastic multi-armed bandit (MAB) problem motivated by ``large'' action spaces, and endowed with a population of arms containing exactly $K$ arm-types, each characterized by a distinct mean reward. The decision maker is oblivious to the statistical properties of reward distributions as well as the population-level distribution of different arm-types, and is precluded also from observing the type of an arm after play. We study the classical problem of minimizing the expected cumulative regret over a horizon of play $n$, and propose algorithms that achieve a rate-optimal finite-time instance-dependent regret of $\mathcal{O}\left( \log n \right)$. We also show that the instance-independent (minimax) regret is $\tilde{\mathcal{O}}\left( \sqrt{n} \right)$ when $K=2$. While the order of regret and complexity of the problem suggests a great degree of similarity to the classical MAB problem, properties of the performance bounds and salient aspects of algorithm design are quite distinct from the latter, as are the key primitives that determine complexity along with the analysis tools needed to study them.

Online Allocation and Learning in the Presence of Strategic Agents

We study the problem of allocating $T$ sequentially arriving items among $n$ homogeneous agents under the constraint that each agent must receive a pre-specified fraction of all items, with the objective of maximizing the agents' total valuation of items allocated to them. The agents' valuations for the item in each round are assumed to be i.i.d. but their distribution is a priori unknown to the central planner. Therefore, the central planner needs to implicitly learn these distributions from the observed values in order to pick a good allocation policy. However, an added challenge here is that the agents are strategic with incentives to misreport their valuations in order to receive better allocations. This sets our work apart both from the online auction design settings which typically assume known valuation distributions and/or involve payments, and from the online learning settings that do not consider strategic agents. To that end, our main contribution is an online learning based allocation mechanism that is approximately Bayesian incentive compatible, and when all agents are truthful, guarantees a sublinear regret for individual agents' utility compared to that under the optimal offline allocation policy.

The Countable-armed Bandit with Vanishing Arms

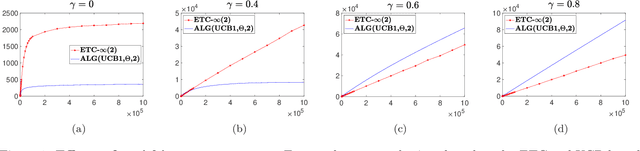
We consider a bandit problem with countably many arms, partitioned into finitely many "types," each characterized by a unique mean reward. A "non-stationary" distribution governs the relative abundance of each arm-type in the population of arms, aka the "arm-reservoir." This non-stationarity is attributable to a probabilistic leakage of "optimal" arms from the reservoir over time, which we refer to as the "vanishing arms" phenomenon; this induces a time-varying (potentially "endogenous," policy-dependent) distribution over the reservoir. The objective is minimization of the expected cumulative regret. We characterize necessary and sufficient conditions for achievability of sub-linear regret in terms of a critical vanishing rate of optimal arms. We also discuss two reservoir distribution-oblivious algorithms that are long-run-average optimal whenever sub-linear regret is statistically achievable. Numerical experiments highlight a distinctive characteristic of this problem related to ex ante knowledge of the "gap" parameter (the difference between the top two mean rewards): in contrast to the stationary bandit formulation, regret in our setting may suffer substantial inflation under adaptive exploration-based (gap-oblivious) algorithms such as UCB vis-`a-vis their non-adaptive forced exploration-based (gap-aware) counterparts like ETC.

A Closer Look at the Worst-case Behavior of Multi-armed Bandit Algorithms

One of the key drivers of complexity in the classical (stochastic) multi-armed bandit (MAB) problem is the difference between mean rewards in the top two arms, also known as the instance gap. The celebrated Upper Confidence Bound (UCB) policy is among the simplest optimism-based MAB algorithms that naturally adapts to this gap: for a horizon of play n, it achieves optimal O(log n) regret in instances with "large" gaps, and a near-optimal O(\sqrt{n log n}) minimax regret when the gap can be arbitrarily "small." This paper provides new results on the arm-sampling behavior of UCB, leading to several important insights. Among these, it is shown that arm-sampling rates under UCB are asymptotically deterministic, regardless of the problem complexity. This discovery facilitates new sharp asymptotics and a novel alternative proof for the O(\sqrt{n log n}) minimax regret of UCB. Furthermore, the paper also provides the first complete process-level characterization of the MAB problem under UCB in the conventional diffusion scaling. Among other things, the "small" gap worst-case lens adopted in this paper also reveals profound distinctions between the behavior of UCB and Thompson Sampling, such as an "incomplete learning" phenomenon characteristic of the latter.

From Finite to Countable-Armed Bandits

We consider a stochastic bandit problem with countably many arms that belong to a finite set of types, each characterized by a unique mean reward. In addition, there is a fixed distribution over types which sets the proportion of each type in the population of arms. The decision maker is oblivious to the type of any arm and to the aforementioned distribution over types, but perfectly knows the total number of types occurring in the population of arms. We propose a fully adaptive online learning algorithm that achieves O(log n) distribution-dependent expected cumulative regret after any number of plays n, and show that this order of regret is best possible. The analysis of our algorithm relies on newly discovered concentration and convergence properties of optimism-based policies like UCB in finite-armed bandit problems with "zero gap," which may be of independent interest.