A Closer Look at the Worst-case Behavior of Multi-armed Bandit Algorithms
Paper and Code
Jun 03, 2021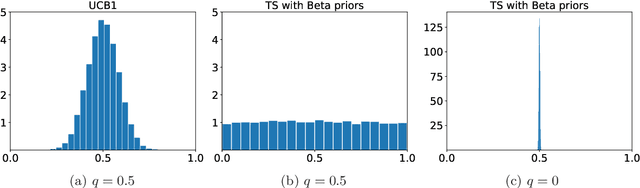
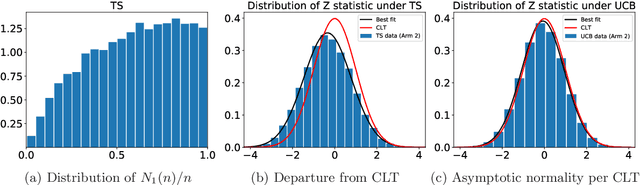
One of the key drivers of complexity in the classical (stochastic) multi-armed bandit (MAB) problem is the difference between mean rewards in the top two arms, also known as the instance gap. The celebrated Upper Confidence Bound (UCB) policy is among the simplest optimism-based MAB algorithms that naturally adapts to this gap: for a horizon of play n, it achieves optimal O(log n) regret in instances with "large" gaps, and a near-optimal O(\sqrt{n log n}) minimax regret when the gap can be arbitrarily "small." This paper provides new results on the arm-sampling behavior of UCB, leading to several important insights. Among these, it is shown that arm-sampling rates under UCB are asymptotically deterministic, regardless of the problem complexity. This discovery facilitates new sharp asymptotics and a novel alternative proof for the O(\sqrt{n log n}) minimax regret of UCB. Furthermore, the paper also provides the first complete process-level characterization of the MAB problem under UCB in the conventional diffusion scaling. Among other things, the "small" gap worst-case lens adopted in this paper also reveals profound distinctions between the behavior of UCB and Thompson Sampling, such as an "incomplete learning" phenomenon characteristic of the latter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge