Last Switch Dependent Bandits with Monotone Payoff Functions

In a recent work, Laforgue et al. introduce the model of last switch dependent (LSD) bandits, in an attempt to capture nonstationary phenomena induced by the interaction between the player and the environment. Examples include satiation, where consecutive plays of the same action lead to decreased performance, or deprivation, where the payoff of an action increases after an interval of inactivity. In this work, we take a step towards understanding the approximability of planning LSD bandits, namely, the (NP-hard) problem of computing an optimal arm-pulling strategy under complete knowledge of the model. In particular, we design the first efficient constant approximation algorithm for the problem and show that, under a natural monotonicity assumption on the payoffs, its approximation guarantee (almost) matches the state-of-the-art for the special and well-studied class of recharging bandits (also known as delay-dependent). In this attempt, we develop new tools and insights for this class of problems, including a novel higher-dimensional relaxation and the technique of mirroring the evolution of virtual states. We believe that these novel elements could potentially be used for approaching richer classes of action-induced nonstationary bandits (e.g., special instances of restless bandits). In the case where the model parameters are initially unknown, we develop an online learning adaptation of our algorithm for which we provide sublinear regret guarantees against its full-information counterpart.

MNL-Bandit in non-stationary environments

In this paper, we study the MNL-Bandit problem in a non-stationary environment and present an algorithm with worst-case dynamic regret of $\tilde{O}\left( \min \left\{ \sqrt{NTL}\;,\; N^{\frac{1}{3}}(\Delta_{\infty}^{K})^{\frac{1}{3}} T^{\frac{2}{3}} + \sqrt{NT}\right\}\right)$. Here $N$ is the number of arms, $L$ is the number of switches and $\Delta_{\infty}^K$ is a variation measure of the unknown parameters. We also show that our algorithm is near-optimal (up to logarithmic factors). Our algorithm builds upon the epoch-based algorithm for stationary MNL-Bandit in Agrawal et al. 2016. However, non-stationarity poses several challenges and we introduce new techniques and ideas to address these. In particular, we give a tight characterization for the bias introduced in the estimators due to non stationarity and derive new concentration bounds.

Interpretable Machine Learning for Resource Allocation with Application to Ventilator Triage

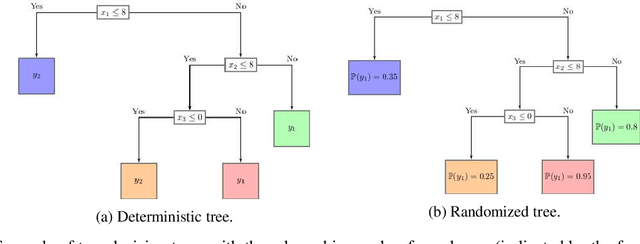
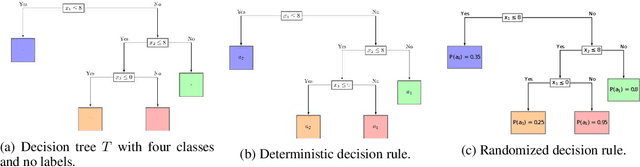
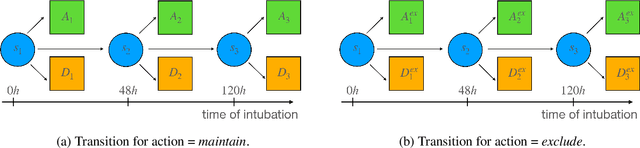
Rationing of healthcare resources is a challenging decision that policy makers and providers may be forced to make during a pandemic, natural disaster, or mass casualty event. Well-defined guidelines to triage scarce life-saving resources must be designed to promote transparency, trust, and consistency. To facilitate buy-in and use during high-stress situations, these guidelines need to be interpretable and operational. We propose a novel data-driven model to compute interpretable triage guidelines based on policies for Markov Decision Process that can be represented as simple sequences of decision trees ("tree policies"). In particular, we characterize the properties of optimal tree policies and present an algorithm based on dynamic programming recursions to compute good tree policies. We utilize this methodology to obtain simple, novel triage guidelines for ventilator allocations for COVID-19 patients, based on real patient data from Montefiore hospitals. We also compare the performance of our guidelines to the official New York State guidelines that were developed in 2015 (well before the COVID-19 pandemic). Our empirical study shows that the number of excess deaths associated with ventilator shortages could be reduced significantly using our policy. Our work highlights the limitations of the existing official triage guidelines, which need to be adapted specifically to COVID-19 before being successfully deployed.

Dynamic pricing and assortment under a contextual MNL demand

We consider dynamic multi-product pricing and assortment problems under an unknown demand over T periods, where in each period, the seller decides on the price for each product or the assortment of products to offer to a customer who chooses according to an unknown Multinomial Logit Model (MNL). Such problems arise in many applications, including online retail and advertising. We propose a randomized dynamic pricing policy based on a variant of the Online Newton Step algorithm (ONS) that achieves a $O(d\sqrt{T}\log(T))$ regret guarantee under an adversarial arrival model. We also present a new optimistic algorithm for the adversarial MNL contextual bandits problem, which achieves a better dependency than the state-of-the-art algorithms in a problem-dependent constant $\kappa$ (potentially exponentially small). Our regret upper bounds scale as $\tilde{O}(d\sqrt{\kappa T}+ \log(T)/\kappa)$, which gives a significantly stronger bound than the existing $\tilde{O}(d\sqrt{T}/\kappa)$ guarantees.

MNL-Bandit with Knapsacks

We consider a dynamic assortment selection problem where a seller has a fixed inventory of $N$ substitutable products and faces an unknown demand that arrives sequentially over $T$ periods. In each period, the seller needs to decide on the assortment of products (of cardinality at most $K$) to offer to the customers. The customer's response follows an unknown multinomial logit model (MNL) with parameters $v$. The goal of the seller is to maximize the total expected revenue given the fixed initial inventory of $N$ products. We give a policy that achieves a regret of $\tilde O\left(K \sqrt{K N T}\left(1 + \frac{\sqrt{v_{\max}}}{q_{\min}}\text{OPT}\right) \right)$ under a mild assumption on the model parameters. In particular, our policy achieves a near-optimal $\tilde O(\sqrt{T})$ regret in the large inventory setting. Our policy builds upon the UCB-based approach for MNL-bandit without inventory constraints in [1] and addresses the inventory constraints through an exponentially sized LP for which we present a tractable approximation while keeping the $\tilde O(\sqrt{T})$ regret bound.

Robust Policies For Proactive ICU Transfers

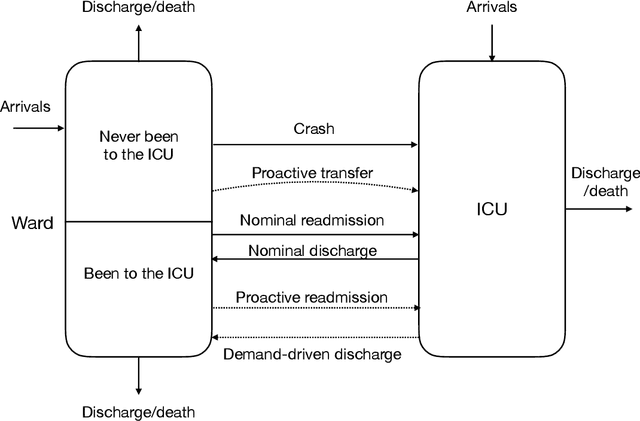
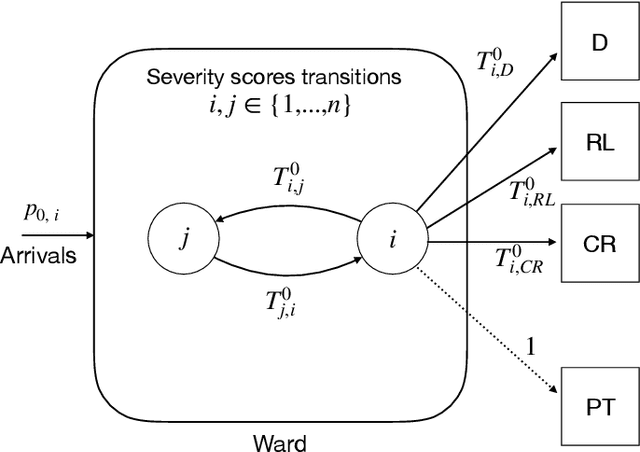
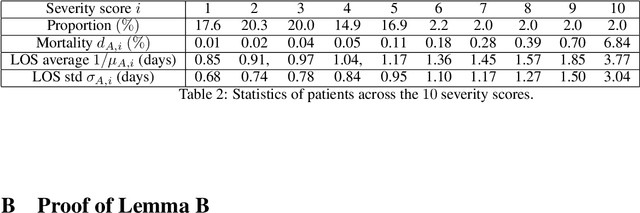
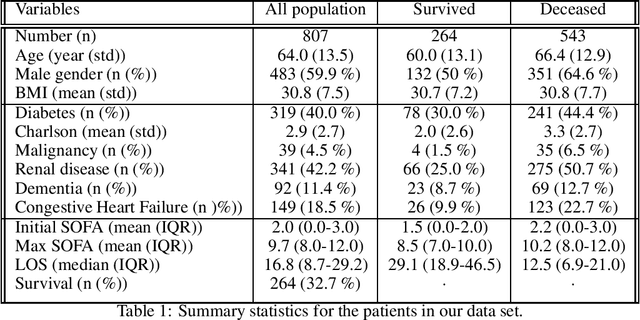
Patients whose transfer to the Intensive Care Unit (ICU) is unplanned are prone to higher mortality rates than those who were admitted directly to the ICU. Recent advances in machine learning to predict patient deterioration have introduced the possibility of \emph{proactive transfer} from the ward to the ICU. In this work, we study the problem of finding \emph{robust} patient transfer policies which account for uncertainty in statistical estimates due to data limitations when optimizing to improve overall patient care. We propose a Markov Decision Process model to capture the evolution of patient health, where the states represent a measure of patient severity. Under fairly general assumptions, we show that an optimal transfer policy has a threshold structure, i.e., that it transfers all patients above a certain severity level to the ICU (subject to available capacity). As model parameters are typically determined based on statistical estimations from real-world data, they are inherently subject to misspecification and estimation errors. We account for this parameter uncertainty by deriving a robust policy that optimizes the worst-case reward across all plausible values of the model parameters. We show that the robust policy also has a threshold structure under fairly general assumptions. Moreover, it is more aggressive in transferring patients than the optimal nominal policy, which does not take into account parameter uncertainty. We present computational experiments using a dataset of hospitalizations at 21 KNPC hospitals, and present empirical evidence of the sensitivity of various hospital metrics (mortality, length-of-stay, average ICU occupancy) to small changes in the parameters. Our work provides useful insights into the impact of parameter uncertainty on deriving simple policies for proactive ICU transfer that have strong empirical performance and theoretical guarantees.

A Generalized Markov Chain Model to Capture Dynamic Preferences and Choice Overload

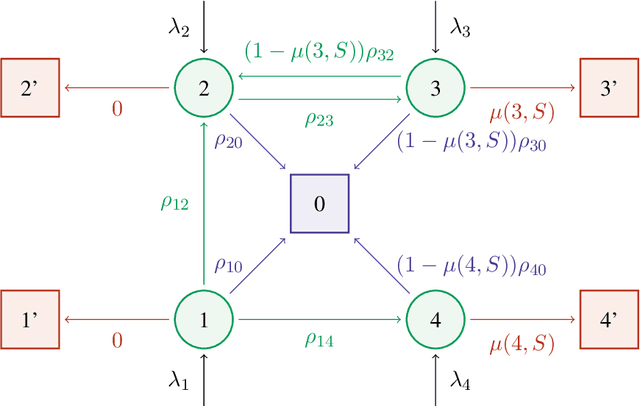
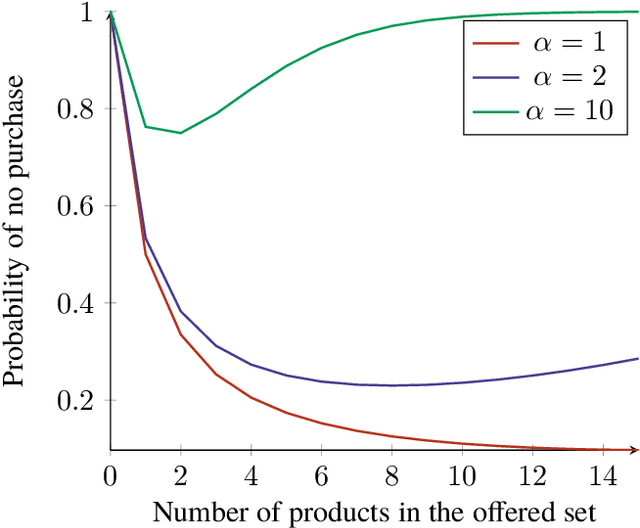
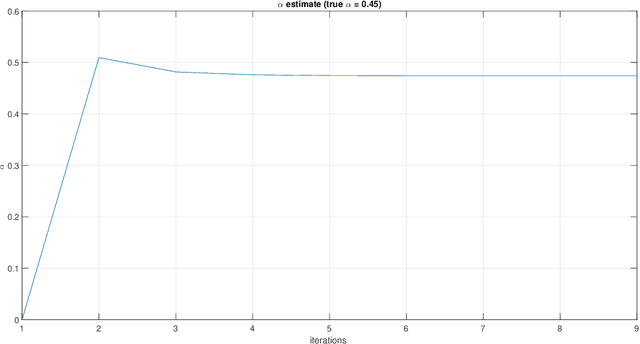
Assortment optimization is an important problem that arises in many practical applications such as retailing and online advertising where the goal is to find a subset of products from a universe of substitutable products that maximize a seller's expected revenue. The demand and the revenue depend on the substitution behavior of the customers that is captured by a choice model. One of the key challenges is to find the right model for the customer substitution behavior. Many parametric random utility based models have been considered in the literature to capture substitution. However, in all these models, the probability of purchase increases as we add more options to the assortment. This is not true in general and in many settings, the probability of purchase may decrease if we add more products to the assortment, referred to as the choice overload. In this paper we attempt to address these serious limitations and propose a generalization of the Markov chain based choice model considered in Blanchet et al. In particular, we handle dynamic preferences and the choice overload phenomenon using a Markovian comparison model that is a generalization of the Markovian substitution framework of Blanchet et al. The Markovian comparison framework allows us to implicitly model the search cost in the choice process and thereby, modeling both dynamic preferences as well as the choice overload phenomenon. We consider the assortment optimization problem for the special case of our generalized Markov chain model where the underlying Markov chain is rank-1 (this is a generalization of the Multinomial Logit model). We show that the assortment optimization problem under this model is NP-hard and present a fully polynomial-time approximation scheme (FPTAS) for this problem.

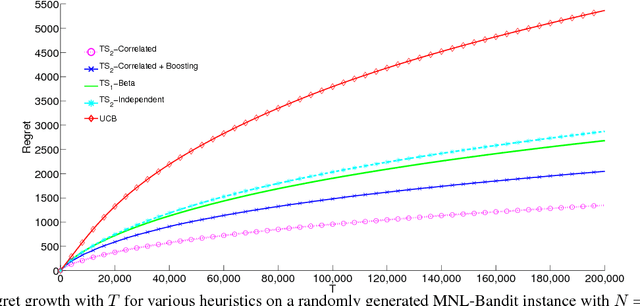
Thompson Sampling for the MNL-Bandit

We consider a sequential subset selection problem under parameter uncertainty, where at each time step, the decision maker selects a subset of cardinality $K$ from $N$ possible items (arms), and observes a (bandit) feedback in the form of the index of one of the items in said subset, or none. Each item in the index set is ascribed a certain value (reward), and the feedback is governed by a Multinomial Logit (MNL) choice model whose parameters are a priori unknown. The objective of the decision maker is to maximize the expected cumulative rewards over a finite horizon $T$, or alternatively, minimize the regret relative to an oracle that knows the MNL parameters. We refer to this as the MNL-Bandit problem. This problem is representative of a larger family of exploration-exploitation problems that involve a combinatorial objective, and arise in several important application domains. We present an approach to adapt Thompson Sampling to this problem and show that it achieves near-optimal regret as well as attractive numerical performance.

MNL-Bandit: A Dynamic Learning Approach to Assortment Selection

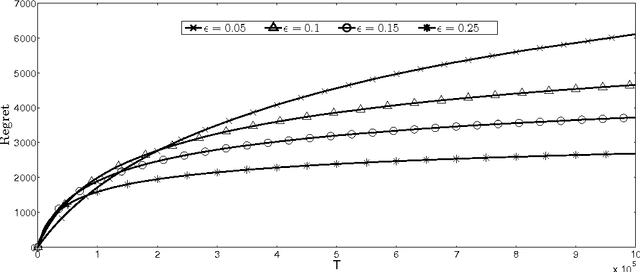
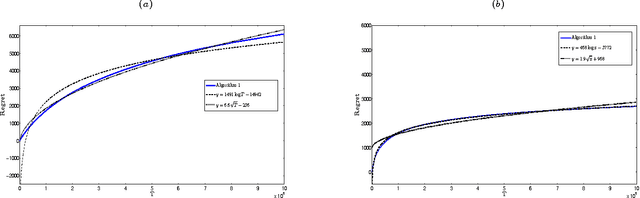
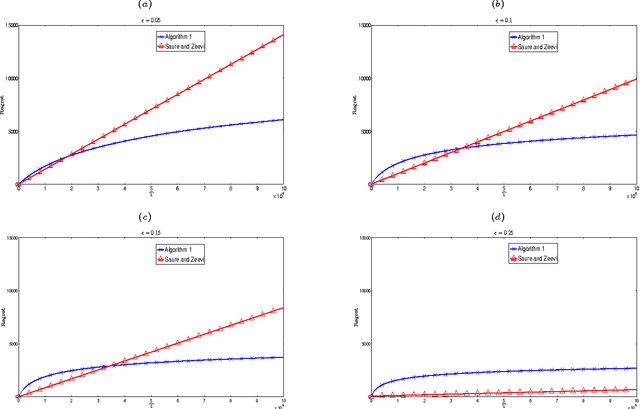
We consider a dynamic assortment selection problem, where in every round the retailer offers a subset (assortment) of $N$ substitutable products to a consumer, who selects one of these products according to a multinomial logit (MNL) choice model. The retailer observes this choice and the objective is to dynamically learn the model parameters, while optimizing cumulative revenues over a selling horizon of length $T$. We refer to this exploration-exploitation formulation as the MNL-Bandit problem. Existing methods for this problem follow an "explore-then-exploit" approach, which estimate parameters to a desired accuracy and then, treating these estimates as if they are the correct parameter values, offers the optimal assortment based on these estimates. These approaches require certain a priori knowledge of "separability", determined by the true parameters of the underlying MNL model, and this in turn is critical in determining the length of the exploration period. (Separability refers to the distinguishability of the true optimal assortment from the other sub-optimal alternatives.) In this paper, we give an efficient algorithm that simultaneously explores and exploits, achieving performance independent of the underlying parameters. The algorithm can be implemented in a fully online manner, without knowledge of the horizon length $T$. Furthermore, the algorithm is adaptive in the sense that its performance is near-optimal in both the "well separated" case, as well as the general parameter setting where this separation need not hold.