Last Switch Dependent Bandits with Monotone Payoff Functions

In a recent work, Laforgue et al. introduce the model of last switch dependent (LSD) bandits, in an attempt to capture nonstationary phenomena induced by the interaction between the player and the environment. Examples include satiation, where consecutive plays of the same action lead to decreased performance, or deprivation, where the payoff of an action increases after an interval of inactivity. In this work, we take a step towards understanding the approximability of planning LSD bandits, namely, the (NP-hard) problem of computing an optimal arm-pulling strategy under complete knowledge of the model. In particular, we design the first efficient constant approximation algorithm for the problem and show that, under a natural monotonicity assumption on the payoffs, its approximation guarantee (almost) matches the state-of-the-art for the special and well-studied class of recharging bandits (also known as delay-dependent). In this attempt, we develop new tools and insights for this class of problems, including a novel higher-dimensional relaxation and the technique of mirroring the evolution of virtual states. We believe that these novel elements could potentially be used for approaching richer classes of action-induced nonstationary bandits (e.g., special instances of restless bandits). In the case where the model parameters are initially unknown, we develop an online learning adaptation of our algorithm for which we provide sublinear regret guarantees against its full-information counterpart.

Non-Stationary Bandits under Recharging Payoffs: Improved Planning with Sublinear Regret

The stochastic multi-armed bandit setting has been recently studied in the non-stationary regime, where the mean payoff of each action is a non-decreasing function of the number of rounds passed since it was last played. This model captures natural behavioral aspects of the users which crucially determine the performance of recommendation platforms, ad placement systems, and more. Even assuming prior knowledge of the mean payoff functions, computing an optimal planning in the above model is NP-hard, while the state-of-the-art is a $1/4$-approximation algorithm for the case where at most one arm can be played per round. We first focus on the setting where the mean payoff functions are known. In this setting, we significantly improve the best-known guarantees for the planning problem by developing a polynomial-time $(1-{1}/{e})$-approximation algorithm (asymptotically and in expectation), based on a novel combination of randomized LP rounding and a time-correlated (interleaved) scheduling method. Furthermore, our algorithm achieves improved guarantees -- compared to prior work -- for the case where more than one arm can be played at each round. Moving to the bandit setting, when the mean payoff functions are initially unknown, we show how our algorithm can be transformed into a bandit algorithm with sublinear regret.

Contextual Pandora's Box

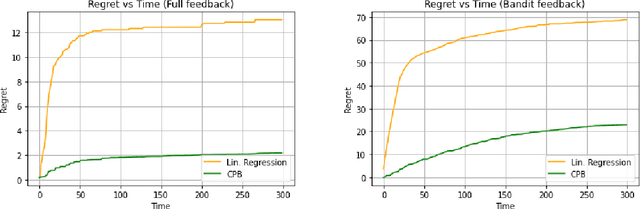
Pandora's Box is a fundamental stochastic optimization problem, where the decision-maker must find a good alternative while minimizing the search cost of exploring the value of each alternative. In the original formulation, it is assumed that accurate priors are given for the values of all the alternatives, while recent work studies the online variant of Pandora's Box where priors are originally unknown. In this work, we extend Pandora's Box to the online setting, while incorporating context. At every round, we are presented with a number of alternatives each having a context, an exploration cost and an unknown value drawn from an unknown prior distribution that may change at every round. Our main result is a no-regret algorithm that performs comparably well to the optimal algorithm which knows all prior distributions exactly. Our algorithm works even in the bandit setting where the algorithm never learns the values of the alternatives that were not explored. The key technique that enables our result is novel a modification of the realizability condition in contextual bandits that connects a context to the reservation value of the corresponding distribution rather than its mean

Combinatorial Blocking Bandits with Stochastic Delays

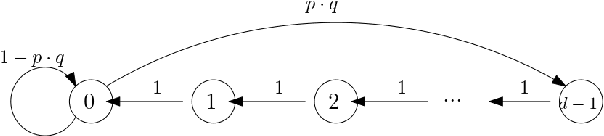
Recent work has considered natural variations of the multi-armed bandit problem, where the reward distribution of each arm is a special function of the time passed since its last pulling. In this direction, a simple (yet widely applicable) model is that of blocking bandits, where an arm becomes unavailable for a deterministic number of rounds after each play. In this work, we extend the above model in two directions: (i) We consider the general combinatorial setting where more than one arms can be played at each round, subject to feasibility constraints. (ii) We allow the blocking time of each arm to be stochastic. We first study the computational/unconditional hardness of the above setting and identify the necessary conditions for the problem to become tractable (even in an approximate sense). Based on these conditions, we provide a tight analysis of the approximation guarantee of a natural greedy heuristic that always plays the maximum expected reward feasible subset among the available (non-blocked) arms. When the arms' expected rewards are unknown, we adapt the above heuristic into a bandit algorithm, based on UCB, for which we provide sublinear (approximate) regret guarantees, matching the theoretical lower bounds in the limiting case of absence of delays.

Recurrent Submodular Welfare and Matroid Blocking Bandits

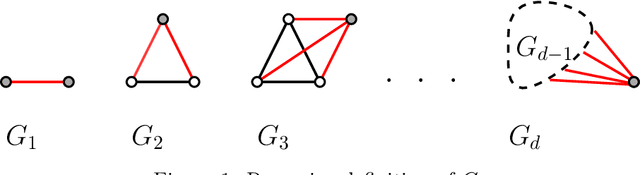
A recent line of research focuses on the study of the stochastic multi-armed bandits problem (MAB), in the case where temporal correlations of specific structure are imposed between the player's actions and the reward distributions of the arms (Kleinberg and Immorlica [FOCS18], Basu et al. [NeurIPS19]). As opposed to the standard MAB setting, where the optimal solution in hindsight can be trivially characterized, these correlations lead to (sub-)optimal solutions that exhibit interesting dynamical patterns -- a phenomenon that yields new challenges both from an algorithmic as well as a learning perspective. In this work, we extend the above direction to a combinatorial bandit setting and study a variant of stochastic MAB, where arms are subject to matroid constraints and each arm becomes unavailable (blocked) for a fixed number of rounds after each play. A natural common generalization of the state-of-the-art for blocking bandits, and that for matroid bandits, yields a $(1-\frac{1}{e})$-approximation for partition matroids, yet it only guarantees a $\frac{1}{2}$-approximation for general matroids. In this paper we develop new algorithmic ideas that allow us to obtain a polynomial-time $(1 - \frac{1}{e})$-approximation algorithm (asymptotically and in expectation) for any matroid, and thus to control the $(1-\frac{1}{e})$-approximate regret. A key ingredient is the technique of correlated (interleaved) scheduling. Along the way, we discover an interesting connection to a variant of Submodular Welfare Maximization, for which we provide (asymptotically) matching upper and lower approximability bounds.

Contextual Blocking Bandits

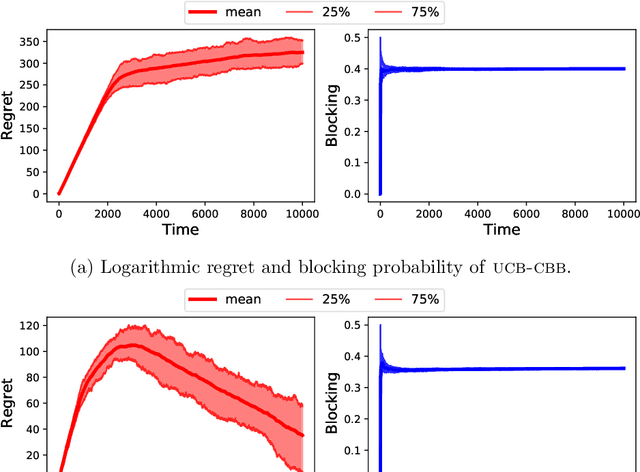
We study a novel variant of the multi-armed bandit problem, where at each time step, the player observes a context that determines the arms' mean rewards. However, playing an arm blocks it (across all contexts) for a fixed number of future time steps. This model extends the blocking bandits model (Basu et al., NeurIPS19) to a contextual setting, and captures important scenarios such as recommendation systems or ad placement with diverse users, and processing diverse pool of jobs. This contextual setting, however, invalidates greedy solution techniques that are effective for its non-contextual counterpart. Assuming knowledge of the mean reward for each arm-context pair, we design a randomized LP-based algorithm which is $\alpha$-optimal in (large enough) $T$ time steps, where $\alpha = \tfrac{d_{\max}}{2d_{\max}-1}\left(1- \epsilon\right)$ for any $\epsilon >0$, and $d_{max}$ is the maximum delay of the arms. In the bandit setting, we show that a UCB based variant of the above online policy guarantees $\mathcal{O}\left(\log T\right)$ regret w.r.t. the $\alpha$-optimal strategy in $T$ time steps, which matches the $\Omega(\log(T))$ regret lower bound in this setting. Due to the time correlation caused by the blocking of arms, existing techniques for upper bounding regret fail. As a first, in the presence of such temporal correlations, we combine ideas from coupling of non-stationary Markov chains and opportunistic sub-sampling with suboptimality charging techniques from combinatorial bandits to prove our regret upper bounds.