Competing Bandits in Decentralized Large Contextual Matching Markets

Sequential learning in a multi-agent resource constrained matching market has received significant interest in the past few years. We study decentralized learning in two-sided matching markets where the demand side (aka players or agents) competes for a `large' supply side (aka arms) with potentially time-varying preferences, to obtain a stable match. Despite a long line of work in the recent past, existing learning algorithms such as Explore-Then-Commit or Upper-Confidence-Bound remain inefficient for this problem. In particular, the per-agent regret achieved by these algorithms scales linearly with the number of arms, $K$. Motivated by the linear contextual bandit framework, we assume that for each agent an arm-mean can be represented by a linear function of a known feature vector and an unknown (agent-specific) parameter. Moreover, our setup captures the essence of a dynamic (non-stationary) matching market where the preferences over arms change over time. Our proposed algorithms achieve instance-dependent logarithmic regret, scaling independently of the number of arms, $K$.

A Statistical Framework for Data-dependent Retrieval-Augmented Models

Modern ML systems increasingly augment input instances with additional relevant information to enhance final prediction. Despite growing interest in such retrieval-augmented models, their fundamental properties and training are not well understood. We propose a statistical framework to study such models with two components: 1) a {\em retriever} to identify the relevant information out of a large corpus via a data-dependent metric; and 2) a {\em predictor} that consumes the input instances along with the retrieved information to make the final predictions. We present a principled method for end-to-end training of both components and draw connections with various training approaches in the literature. Furthermore, we establish excess risk bounds for retrieval-augmented models while delineating the contributions of both retriever and predictor towards the model performance. We validate the utility of our proposed training methods along with the key takeaways from our statistical analysis on open domain question answering task where retrieval augmentation is important.

Generalization Properties of Retrieval-based Models

Many modern high-performing machine learning models such as GPT-3 primarily rely on scaling up models, e.g., transformer networks. Simultaneously, a parallel line of work aims to improve the model performance by augmenting an input instance with other (labeled) instances during inference. Examples of such augmentations include task-specific prompts and similar examples retrieved from the training data by a nonparametric component. Remarkably, retrieval-based methods have enjoyed success on a wide range of problems, ranging from standard natural language processing and vision tasks to protein folding, as demonstrated by many recent efforts, including WebGPT and AlphaFold. Despite growing literature showcasing the promise of these models, the theoretical underpinning for such models remains underexplored. In this paper, we present a formal treatment of retrieval-based models to characterize their generalization ability. In particular, we focus on two classes of retrieval-based classification approaches: First, we analyze a local learning framework that employs an explicit local empirical risk minimization based on retrieved examples for each input instance. Interestingly, we show that breaking down the underlying learning task into local sub-tasks enables the model to employ a low complexity parametric component to ensure good overall accuracy. The second class of retrieval-based approaches we explore learns a global model using kernel methods to directly map an input instance and retrieved examples to a prediction, without explicitly solving a local learning task.

Double Auctions with Two-sided Bandit Feedback

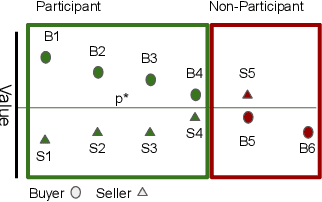
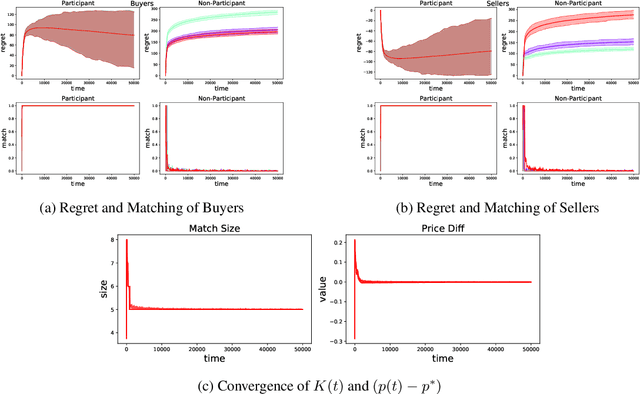
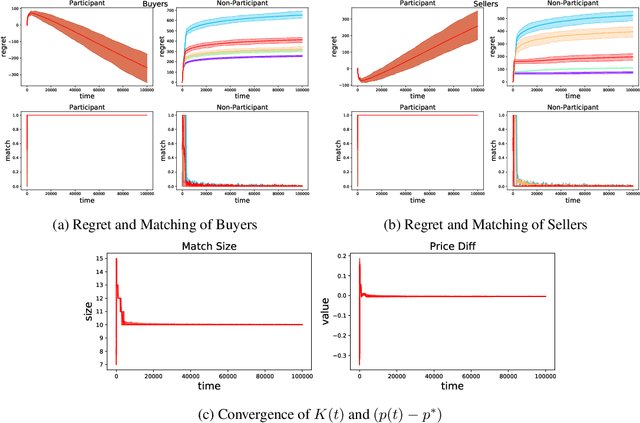
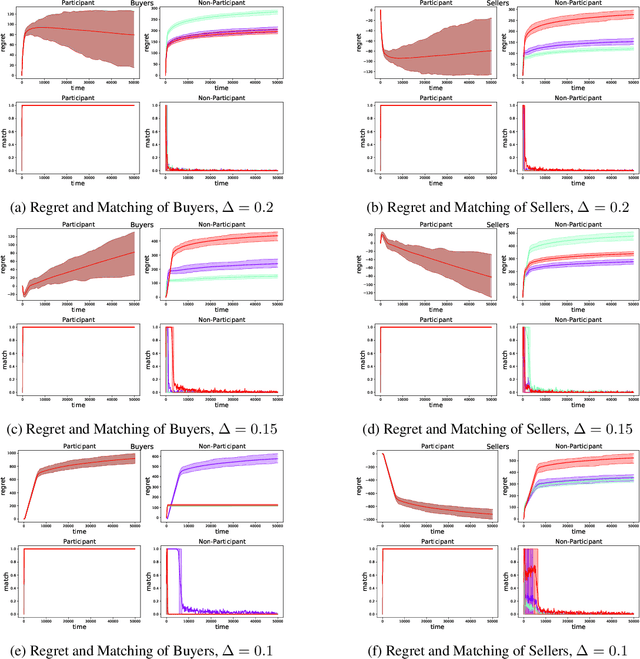
Double Auction enables decentralized transfer of goods between multiple buyers and sellers, thus underpinning functioning of many online marketplaces. Buyers and sellers compete in these markets through bidding, but do not often know their own valuation a-priori. As the allocation and pricing happens through bids, the profitability of participants, hence sustainability of such markets, depends crucially on learning respective valuations through repeated interactions. We initiate the study of Double Auction markets under bandit feedback on both buyers' and sellers' side. We show with confidence bound based bidding, and `Average Pricing' there is an efficient price discovery among the participants. In particular, the buyers and sellers exchanging goods attain $O(\sqrt{T})$ regret in $T$ rounds. The buyers and sellers who do not benefit from exchange in turn only experience $O(\log{T}/ \Delta)$ regret in $T$ rounds where $\Delta$ is the minimum price gap. We augment our upper bound by showing that even with a known fixed price of the good -- a simpler learning problem than Double Auction -- $\omega(\sqrt{T})$ regret is unattainable in certain markets.

No Regrets for Learning the Prior in Bandits

We propose ${\tt AdaTS}$, a Thompson sampling algorithm that adapts sequentially to bandit tasks that it interacts with. The key idea in ${\tt AdaTS}$ is to adapt to an unknown task prior distribution by maintaining a distribution over its parameters. When solving a bandit task, that uncertainty is marginalized out and properly accounted for. ${\tt AdaTS}$ is a fully-Bayesian algorithm that can be implemented efficiently in several classes of bandit problems. We derive upper bounds on its Bayes regret that quantify the loss due to not knowing the task prior, and show that it is small. Our theory is supported by experiments, where ${\tt AdaTS}$ outperforms prior algorithms and works well even in challenging real-world problems.

Episodic Bandits with Stochastic Experts

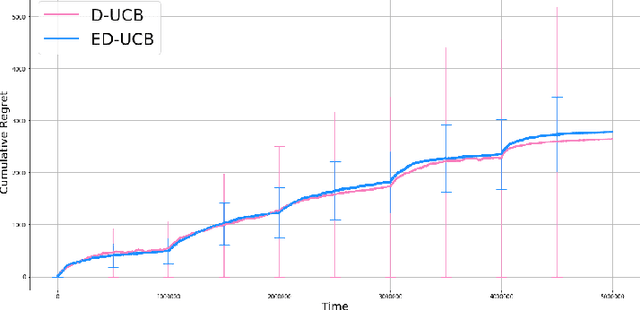
We study a version of the contextual bandit problem where an agent is given soft control of a node in a graph-structured environment through a set of stochastic expert policies. The agent interacts with the environment over episodes, with each episode having different context distributions; this results in the `best expert' changing across episodes. Our goal is to develop an agent that tracks the best expert over episodes. We introduce the Empirical Divergence-based UCB (ED-UCB) algorithm in this setting where the agent does not have any knowledge of the expert policies or changes in context distributions. With mild assumptions, we show that bootstrapping from $\tilde{O}(N\log(NT^2\sqrt{E}))$ samples results in a regret of $\tilde{O}(E(N+1) + \frac{N\sqrt{E}}{T^2})$. If the expert policies are known to the agent a priori, then we can improve the regret to $\tilde{O}(EN)$ without requiring any bootstrapping. Our analysis also tightens pre-existing logarithmic regret bounds to a problem-dependent constant in the non-episodic setting when expert policies are known. We finally empirically validate our findings through simulations.

Combinatorial Blocking Bandits with Stochastic Delays

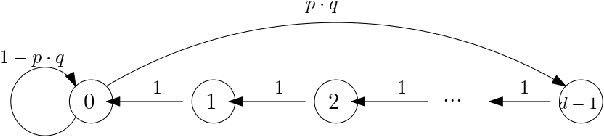
Recent work has considered natural variations of the multi-armed bandit problem, where the reward distribution of each arm is a special function of the time passed since its last pulling. In this direction, a simple (yet widely applicable) model is that of blocking bandits, where an arm becomes unavailable for a deterministic number of rounds after each play. In this work, we extend the above model in two directions: (i) We consider the general combinatorial setting where more than one arms can be played at each round, subject to feasibility constraints. (ii) We allow the blocking time of each arm to be stochastic. We first study the computational/unconditional hardness of the above setting and identify the necessary conditions for the problem to become tractable (even in an approximate sense). Based on these conditions, we provide a tight analysis of the approximation guarantee of a natural greedy heuristic that always plays the maximum expected reward feasible subset among the available (non-blocked) arms. When the arms' expected rewards are unknown, we adapt the above heuristic into a bandit algorithm, based on UCB, for which we provide sublinear (approximate) regret guarantees, matching the theoretical lower bounds in the limiting case of absence of delays.

Beyond $\log^2$ Regret for Decentralized Bandits in Matching Markets

We design decentralized algorithms for regret minimization in the two-sided matching market with one-sided bandit feedback that significantly improves upon the prior works (Liu et al. 2020a, 2020b, Sankararaman et al. 2020). First, for general markets, for any $\varepsilon > 0$, we design an algorithm that achieves a $O(\log^{1+\varepsilon}(T))$ regret to the agent-optimal stable matching, with unknown time horizon $T$, improving upon the $O(\log^{2}(T))$ regret achieved in (Liu et al. 2020b). Second, we provide the optimal $\Theta(\log(T))$ agent-optimal regret for markets satisfying uniqueness consistency -- markets where leaving participants don't alter the original stable matching. Previously, $\Theta(\log(T))$ regret was achievable (Sankararaman et al. 2020, Liu et al. 2020b) in the much restricted serial dictatorship setting, when all arms have the same preference over the agents. We propose a phase-based algorithm, wherein each phase, besides deleting the globally communicated dominated arms the agents locally delete arms with which they collide often. This local deletion is pivotal in breaking deadlocks arising from rank heterogeneity of agents across arms. We further demonstrate the superiority of our algorithm over existing works through simulations.

Robust Estimation of Tree Structured Markov Random Fields

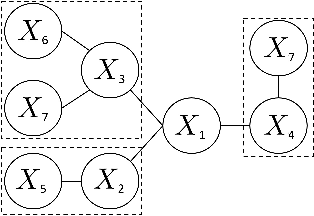
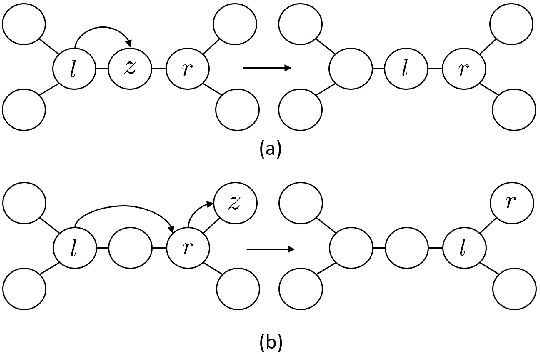
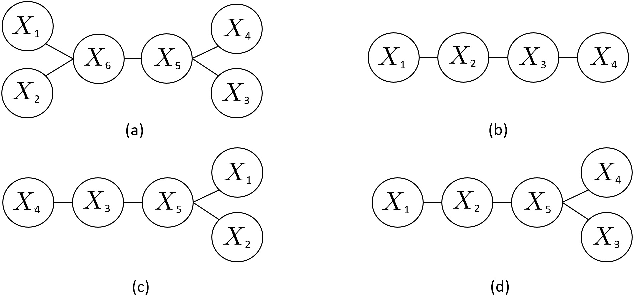
We study the problem of learning tree-structured Markov random fields (MRF) on discrete random variables with common support when the observations are corrupted by unknown noise. As the presence of noise in the observations obfuscates the original tree structure, the extent of recoverability of the tree-structured MRFs under noisy observations is brought into question. We show that in a general noise model, the underlying tree structure can be recovered only up to an equivalence class where each of the leaf nodes is indistinguishable from its parent and siblings, forming a leaf cluster. As the indistinguishability arises due to contrived noise models, we study the natural k-ary symmetric channel noise model where the value of each node is changed to a uniform value in the support with an unequal and unknown probability. Here, the answer becomes much more nuanced. We show that with a support size of 2, and the binary symmetric channel noise model, the leaf clusters remain indistinguishable. From support size 3 and up, the recoverability of a leaf cluster is dictated by the joint probability mass function of the nodes within it. We provide a precise characterization of recoverability by deriving a necessary and sufficient condition for the recoverability of a leaf cluster. We provide an algorithm that recovers the tree if this condition is satisfied, and recovers the tree up to the leaf clusters failing this condition.

On Generalization of Adaptive Methods for Over-parameterized Linear Regression

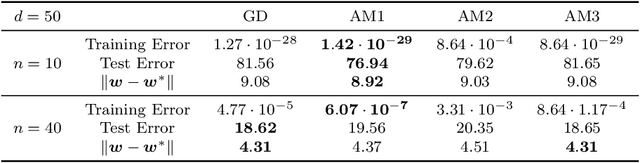
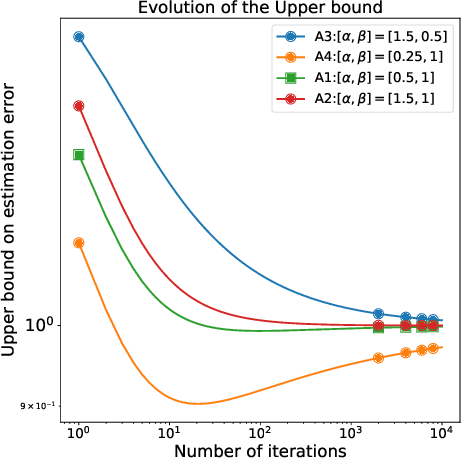
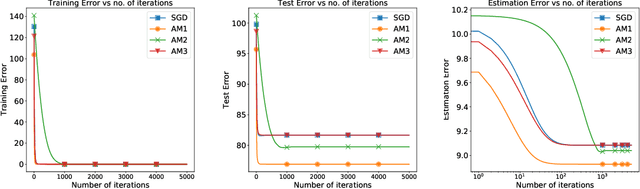
Over-parameterization and adaptive methods have played a crucial role in the success of deep learning in the last decade. The widespread use of over-parameterization has forced us to rethink generalization by bringing forth new phenomena, such as implicit regularization of optimization algorithms and double descent with training progression. A series of recent works have started to shed light on these areas in the quest to understand -- why do neural networks generalize well? The setting of over-parameterized linear regression has provided key insights into understanding this mysterious behavior of neural networks. In this paper, we aim to characterize the performance of adaptive methods in the over-parameterized linear regression setting. First, we focus on two sub-classes of adaptive methods depending on their generalization performance. For the first class of adaptive methods, the parameter vector remains in the span of the data and converges to the minimum norm solution like gradient descent (GD). On the other hand, for the second class of adaptive methods, the gradient rotation caused by the pre-conditioner matrix results in an in-span component of the parameter vector that converges to the minimum norm solution and the out-of-span component that saturates. Our experiments on over-parameterized linear regression and deep neural networks support this theory.