The Hidden Bias of Process Reward Models:PRISM for Rewarding the Right Reasoning

Process Reward Models (PRMs) improve credit assignment for reasoning by providing step-level feedback. However, we identify a hidden bias in PRMs caused by severe imbalance in step-level training data. Standard cross-entropy training amplifies this bias, causing PRMs to overcredit plausible but incorrect steps and produce high false-positive rates. We show that these false positives have an asymmetric downstream effect: false negatives mainly slow exploration, whereas false positives actively steer Best-of-N selection, guided decoding, and policy optimization toward flawed reasoning. This suggests that PRM training should shift from pointwise label fitting to reliable relative comparisons. To address this, we propose PRISM (Precision Ranking for Improved Step Modeling), a policy-aware PRM training framework that learns from contrastive step-level comparisons and hard negatives generated by a temporal lookahead strategy, requiring no new human labels. We further use a difficulty-aware curriculum to optimize the contrastive step margin. Across PRMBench and ProcessBench, PRISM substantially reduces false positives (22% on PRMBench) and improves macro F1 over strong discriminative PRMs. When applied to policy optimization and search tasks, including guided decoding and Best-of-N selection, it consistently improves accuracy (up to 22% for guided decoding and 33% for Best-of-N) and robustness. More broadly, trustworthy process supervision is not just about assigning high rewards, but about rewarding the right reasoning for the right reasons.

Zero-shot Multivariate Time Series Forecasting Using Tabular Prior Fitted Networks

Tabular foundation models, particularly Prior-data Fitted Networks like TabPFN have emerged as the leading contender in a myriad of tasks ranging from data imputation to label prediction on the tabular data format surpassing the historical successes of tree-based models. This has led to investigations on their applicability to forecasting time series data which can be formulated as a tabular problem. While recent work to this end has displayed positive results, most works have limited their treatment of multivariate time series problems to several independent univariate time series forecasting subproblems, thus ignoring any inter-channel interactions. Overcoming this limitation, we introduce a generally applicable framework for multivariate time series forecasting using tabular foundation models. We achieve this by recasting the multivariate time series forecasting problem as a series of scalar regression problems which can then be solved zero-shot by any tabular foundation model with regression capabilities. We present results of our method using the TabPFN-TS backbone and compare performance with the current state of the art tabular methods.

On a Foundation Model for Operating Systems

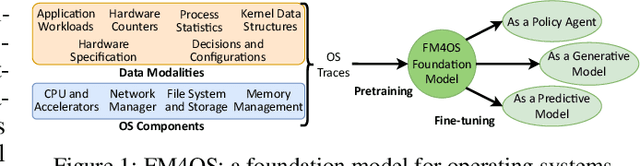
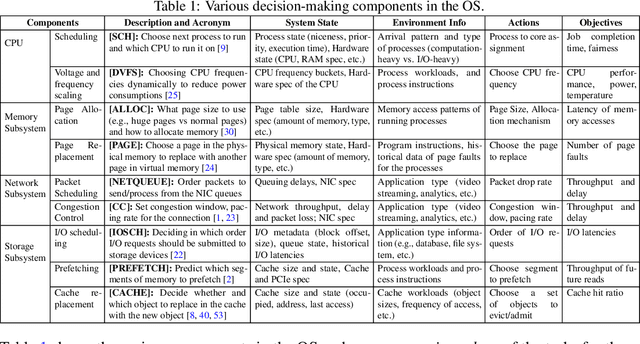
This paper lays down the research agenda for a domain-specific foundation model for operating systems (OSes). Our case for a foundation model revolves around the observations that several OS components such as CPU, memory, and network subsystems are interrelated and that OS traces offer the ideal dataset for a foundation model to grasp the intricacies of diverse OS components and their behavior in varying environments and workloads. We discuss a wide range of possibilities that then arise, from employing foundation models as policy agents to utilizing them as generators and predictors to assist traditional OS control algorithms. Our hope is that this paper spurs further research into OS foundation models and creating the next generation of operating systems for the evolving computing landscape.

Episodic Bandits with Stochastic Experts

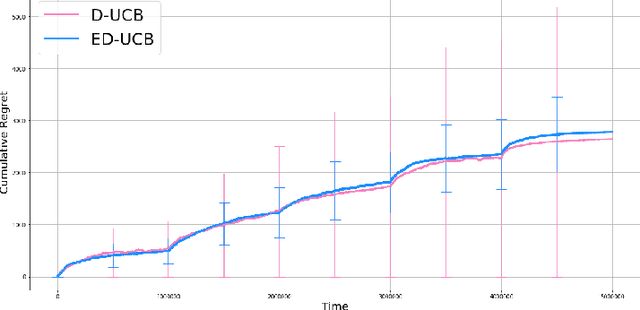
We study a version of the contextual bandit problem where an agent is given soft control of a node in a graph-structured environment through a set of stochastic expert policies. The agent interacts with the environment over episodes, with each episode having different context distributions; this results in the `best expert' changing across episodes. Our goal is to develop an agent that tracks the best expert over episodes. We introduce the Empirical Divergence-based UCB (ED-UCB) algorithm in this setting where the agent does not have any knowledge of the expert policies or changes in context distributions. With mild assumptions, we show that bootstrapping from $\tilde{O}(N\log(NT^2\sqrt{E}))$ samples results in a regret of $\tilde{O}(E(N+1) + \frac{N\sqrt{E}}{T^2})$. If the expert policies are known to the agent a priori, then we can improve the regret to $\tilde{O}(EN)$ without requiring any bootstrapping. Our analysis also tightens pre-existing logarithmic regret bounds to a problem-dependent constant in the non-episodic setting when expert policies are known. We finally empirically validate our findings through simulations.

Warm Starting Bandits with Side Information from Confounded Data

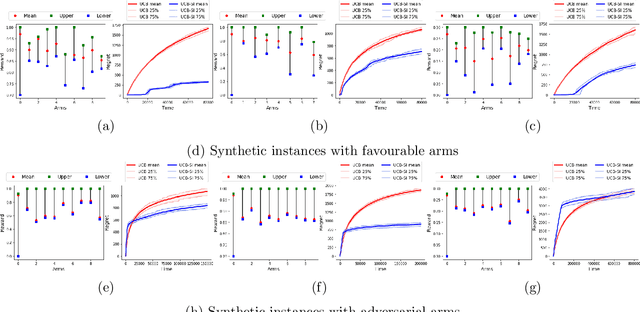
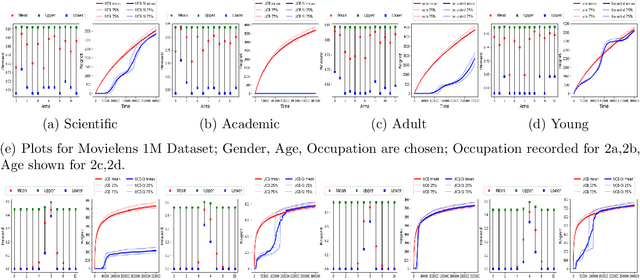
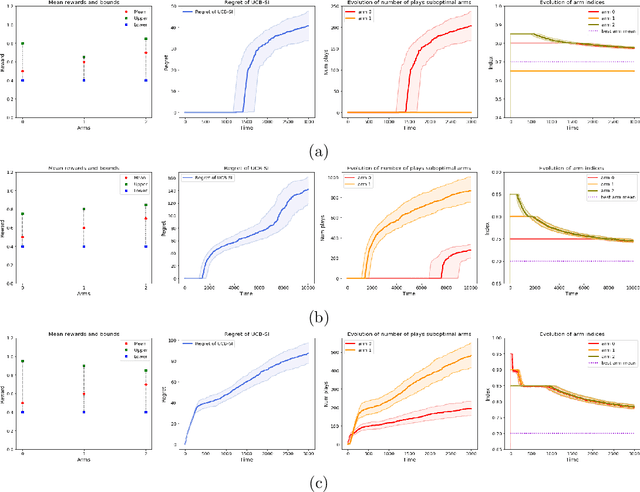
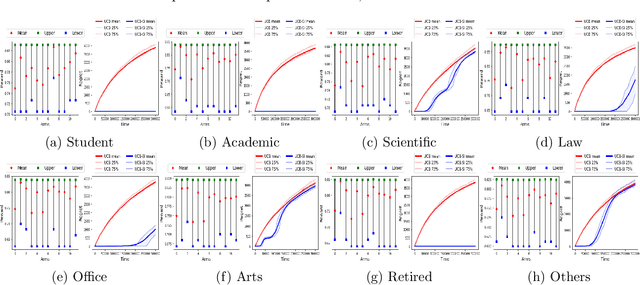
We study a variant of the multi-armed bandit problem where side information in the form of bounds on the mean of each arm is provided. We describe how these bounds on the means can be used efficiently for warm starting bandits. Specifically, we propose the novel UCB-SI algorithm, and illustrate improvements in cumulative regret over the standard UCB algorithm, both theoretically and empirically, in the presence of non-trivial side information. As noted in (Zhang & Bareinboim, 2017), such information arises, for instance, when we have prior logged data on the arms, but this data has been collected under a policy whose choice of arms is based on latent variables to which access is no longer available. We further provide a novel approach for obtaining such bounds from prior partially confounded data under some mild assumptions. We validate our findings through semi-synthetic experiments on data derived from real datasets.