Warm Starting Bandits with Side Information from Confounded Data

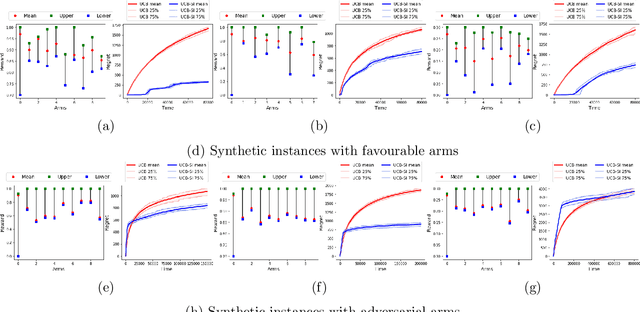
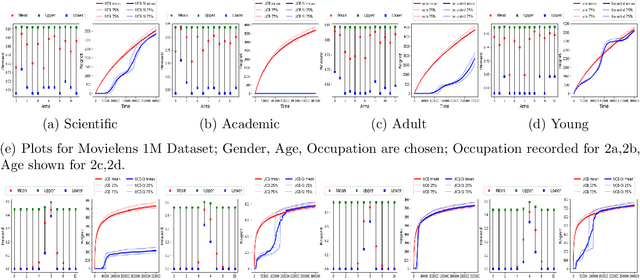
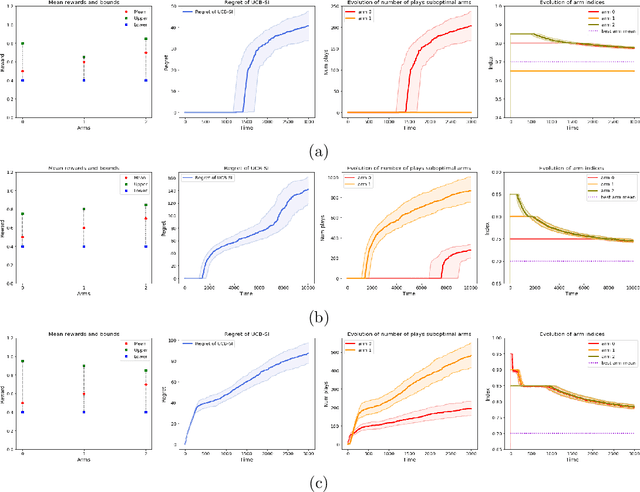
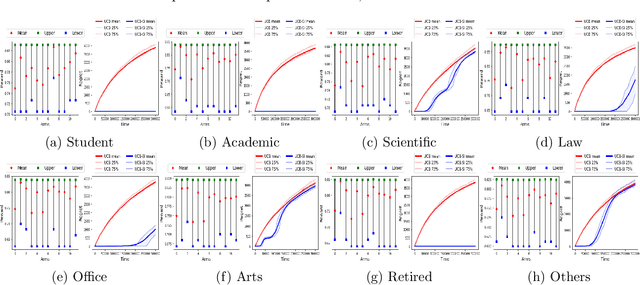
We study a variant of the multi-armed bandit problem where side information in the form of bounds on the mean of each arm is provided. We describe how these bounds on the means can be used efficiently for warm starting bandits. Specifically, we propose the novel UCB-SI algorithm, and illustrate improvements in cumulative regret over the standard UCB algorithm, both theoretically and empirically, in the presence of non-trivial side information. As noted in (Zhang & Bareinboim, 2017), such information arises, for instance, when we have prior logged data on the arms, but this data has been collected under a policy whose choice of arms is based on latent variables to which access is no longer available. We further provide a novel approach for obtaining such bounds from prior partially confounded data under some mild assumptions. We validate our findings through semi-synthetic experiments on data derived from real datasets.