Episodic Bandits with Stochastic Experts
Paper and Code
Jul 07, 2021
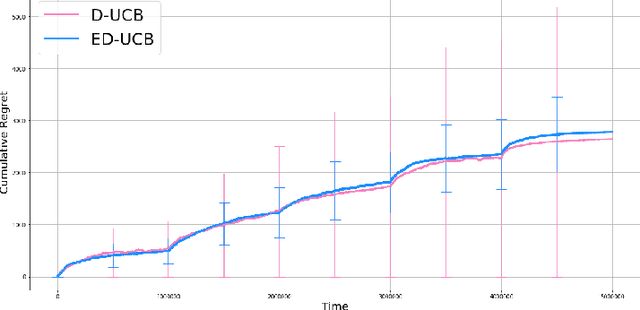
We study a version of the contextual bandit problem where an agent is given soft control of a node in a graph-structured environment through a set of stochastic expert policies. The agent interacts with the environment over episodes, with each episode having different context distributions; this results in the `best expert' changing across episodes. Our goal is to develop an agent that tracks the best expert over episodes. We introduce the Empirical Divergence-based UCB (ED-UCB) algorithm in this setting where the agent does not have any knowledge of the expert policies or changes in context distributions. With mild assumptions, we show that bootstrapping from $\tilde{O}(N\log(NT^2\sqrt{E}))$ samples results in a regret of $\tilde{O}(E(N+1) + \frac{N\sqrt{E}}{T^2})$. If the expert policies are known to the agent a priori, then we can improve the regret to $\tilde{O}(EN)$ without requiring any bootstrapping. Our analysis also tightens pre-existing logarithmic regret bounds to a problem-dependent constant in the non-episodic setting when expert policies are known. We finally empirically validate our findings through simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge