SoK: Decentralized AI (DeAI)

The centralization of Artificial Intelligence (AI) poses significant challenges, including single points of failure, inherent biases, data privacy concerns, and scalability issues. These problems are especially prevalent in closed-source large language models (LLMs), where user data is collected and used without transparency. To mitigate these issues, blockchain-based decentralized AI (DeAI) has emerged as a promising solution. DeAI combines the strengths of both blockchain and AI technologies to enhance the transparency, security, decentralization, and trustworthiness of AI systems. However, a comprehensive understanding of state-of-the-art DeAI development, particularly for active industry solutions, is still lacking. In this work, we present a Systematization of Knowledge (SoK) for blockchain-based DeAI solutions. We propose a taxonomy to classify existing DeAI protocols based on the model lifecycle. Based on this taxonomy, we provide a structured way to clarify the landscape of DeAI protocols and identify their similarities and differences. We analyze the functionalities of blockchain in DeAI, investigating how blockchain features contribute to enhancing the security, transparency, and trustworthiness of AI processes, while also ensuring fair incentives for AI data and model contributors. In addition, we identify key insights and research gaps in developing DeAI protocols, highlighting several critical avenues for future research.

Robust Estimation of Tree Structured Markov Random Fields

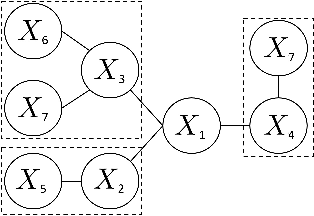
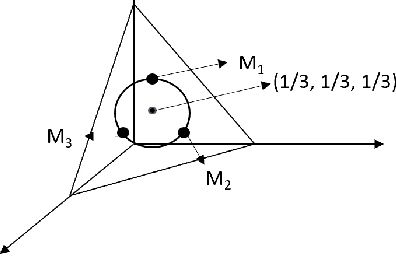
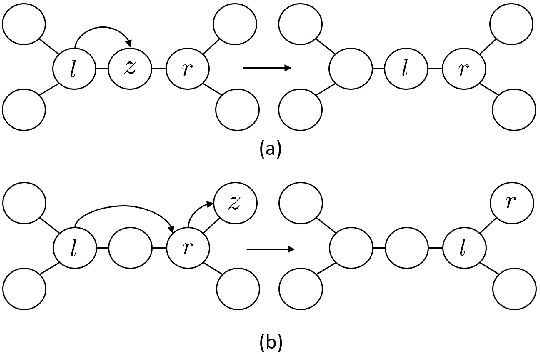
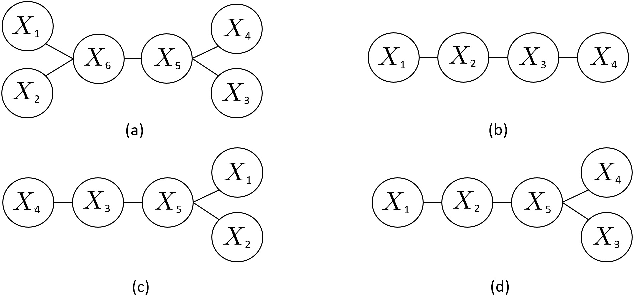
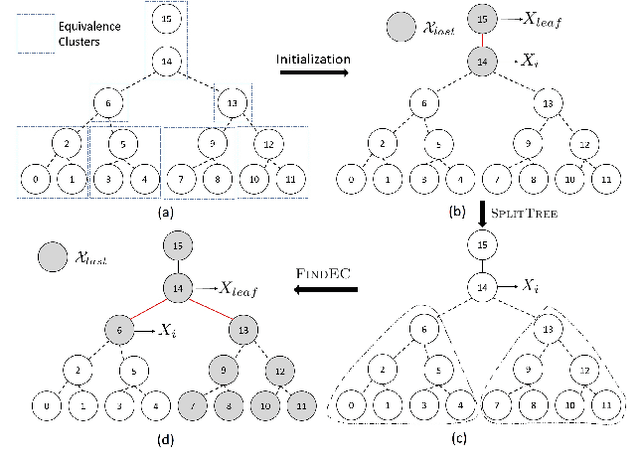
We study the problem of learning tree-structured Markov random fields (MRF) on discrete random variables with common support when the observations are corrupted by unknown noise. As the presence of noise in the observations obfuscates the original tree structure, the extent of recoverability of the tree-structured MRFs under noisy observations is brought into question. We show that in a general noise model, the underlying tree structure can be recovered only up to an equivalence class where each of the leaf nodes is indistinguishable from its parent and siblings, forming a leaf cluster. As the indistinguishability arises due to contrived noise models, we study the natural k-ary symmetric channel noise model where the value of each node is changed to a uniform value in the support with an unequal and unknown probability. Here, the answer becomes much more nuanced. We show that with a support size of 2, and the binary symmetric channel noise model, the leaf clusters remain indistinguishable. From support size 3 and up, the recoverability of a leaf cluster is dictated by the joint probability mass function of the nodes within it. We provide a precise characterization of recoverability by deriving a necessary and sufficient condition for the recoverability of a leaf cluster. We provide an algorithm that recovers the tree if this condition is satisfied, and recovers the tree up to the leaf clusters failing this condition.

On Generalization of Adaptive Methods for Over-parameterized Linear Regression

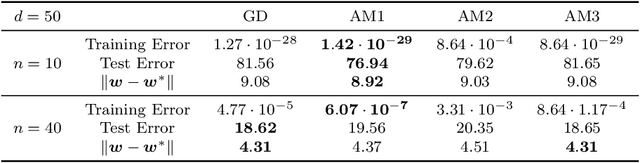
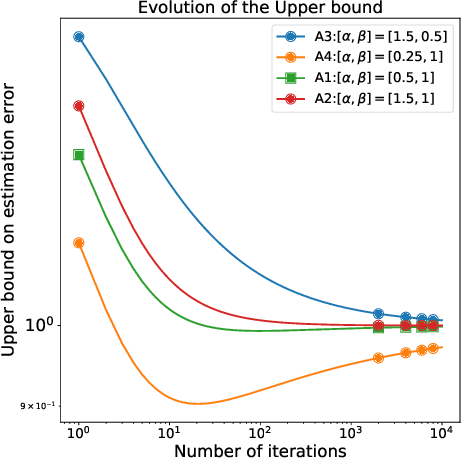
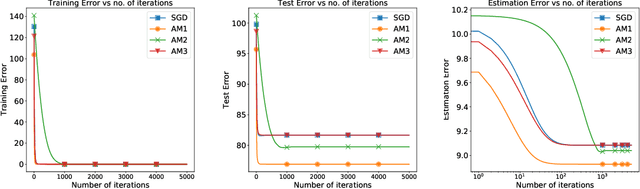
Over-parameterization and adaptive methods have played a crucial role in the success of deep learning in the last decade. The widespread use of over-parameterization has forced us to rethink generalization by bringing forth new phenomena, such as implicit regularization of optimization algorithms and double descent with training progression. A series of recent works have started to shed light on these areas in the quest to understand -- why do neural networks generalize well? The setting of over-parameterized linear regression has provided key insights into understanding this mysterious behavior of neural networks. In this paper, we aim to characterize the performance of adaptive methods in the over-parameterized linear regression setting. First, we focus on two sub-classes of adaptive methods depending on their generalization performance. For the first class of adaptive methods, the parameter vector remains in the span of the data and converges to the minimum norm solution like gradient descent (GD). On the other hand, for the second class of adaptive methods, the gradient rotation caused by the pre-conditioner matrix results in an in-span component of the parameter vector that converges to the minimum norm solution and the out-of-span component that saturates. Our experiments on over-parameterized linear regression and deep neural networks support this theory.

Robust Estimation of Tree Structured Ising Models

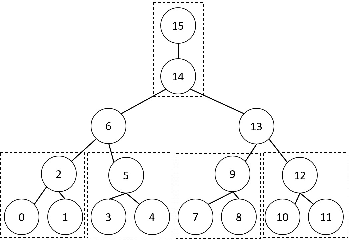
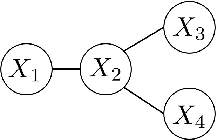
We consider the task of learning Ising models when the signs of different random variables are flipped independently with possibly unequal, unknown probabilities. In this paper, we focus on the problem of robust estimation of tree-structured Ising models. Without any additional assumption of side information, this is an open problem. We first prove that this problem is unidentifiable, however, this unidentifiability is limited to a small equivalence class of trees formed by leaf nodes exchanging positions with their neighbors. Next, we propose an algorithm to solve the above problem with logarithmic sample complexity in the number of nodes and polynomial run-time complexity. Lastly, we empirically demonstrate that, as expected, existing algorithms are not inherently robust in the proposed setting whereas our algorithm correctly recovers the underlying equivalence class.

Choosing the Sample with Lowest Loss makes SGD Robust

The presence of outliers can potentially significantly skew the parameters of machine learning models trained via stochastic gradient descent (SGD). In this paper we propose a simple variant of the simple SGD method: in each step, first choose a set of k samples, then from these choose the one with the smallest current loss, and do an SGD-like update with this chosen sample. Vanilla SGD corresponds to k = 1, i.e. no choice; k >= 2 represents a new algorithm that is however effectively minimizing a non-convex surrogate loss. Our main contribution is a theoretical analysis of the robustness properties of this idea for ML problems which are sums of convex losses; these are backed up with linear regression and small-scale neural network experiments

Negative sampling in semi-supervised learning

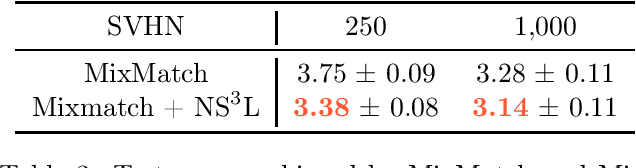
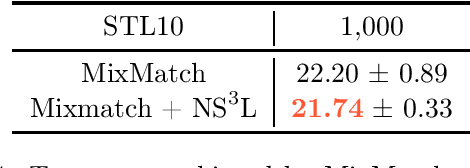
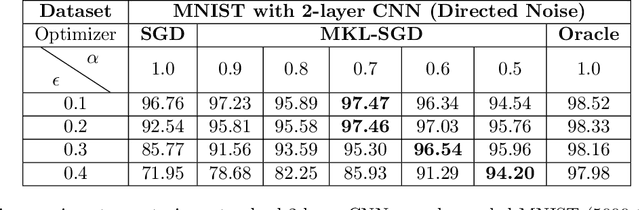
We introduce Negative Sampling in Semi-Supervised Learning (NS3L), a simple, fast, easy to tune algorithm for semi-supervised learning (SSL). NS3L is motivated by the success of negative sampling/contrastive estimation. We demonstrate that adding the NS3L loss to state-of-the-art SSL algorithms, such as the Virtual Adversarial Training (VAT), significantly improves upon vanilla VAT and its variant, VAT with Entropy Minimization. By adding the NS3L loss to MixMatch, the current state-of-the-art approach on semi-supervised tasks, we observe significant improvements over vanilla MixMatch. We conduct extensive experiments on the CIFAR10, CIFAR100, SVHN and STL10 benchmark datasets.

Minimum norm solutions do not always generalize well for over-parameterized problems

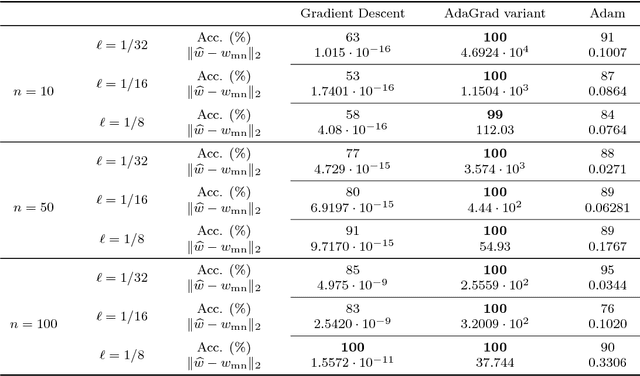
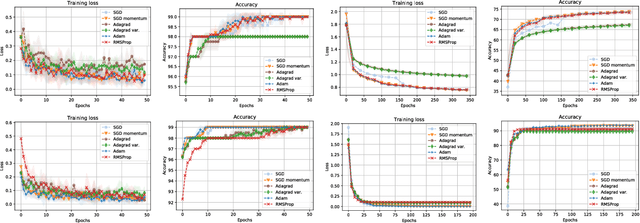
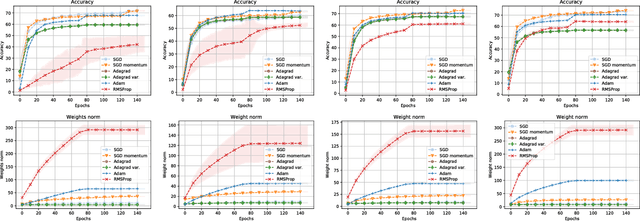
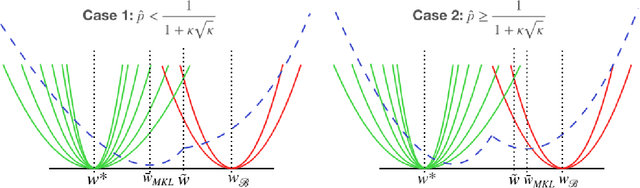
Stochastic gradient descent is the de facto algorithm for training deep neural networks (DNNs). Despite its popularity, it still requires fine hyper-parameter tuning in order to achieve its best performance. This has led to the development of adaptive methods, that claim automatic hyper-parameter tuning. Recently, researchers have studied both algorithmic classes via thoughtful toy problems: e.g., for over-parameterized linear regression, [1] shows that, while SGD always converges to the minimum-norm solution (similar to the case of the maximum margin solution in SVMs that guarantees good prediction error), adaptive methods show no such inclination, leading to worse generalization capabilities. Our aim is to study this conjecture further. We empirically show that the minimum norm solution is not necessarily the proper gauge of good generalization in simplified scenaria, and different models found by adaptive methods could outperform plain gradient methods. In practical DNN settings, we observe that adaptive methods often perform at least as well as SGD, without necessarily reducing the amount of tuning required.

Matrix Completion via Factorizing Polynomials

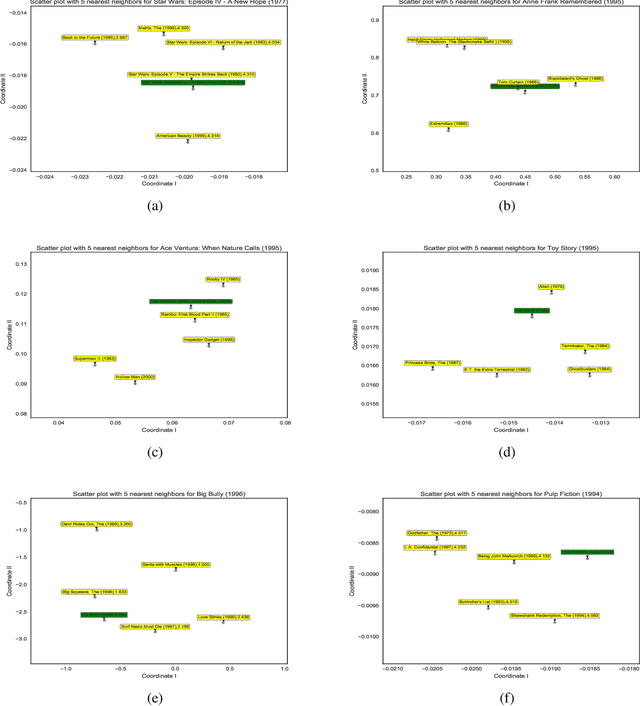
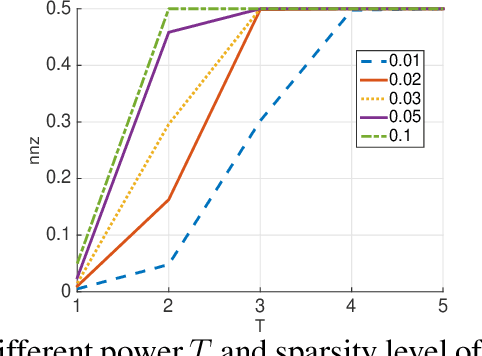
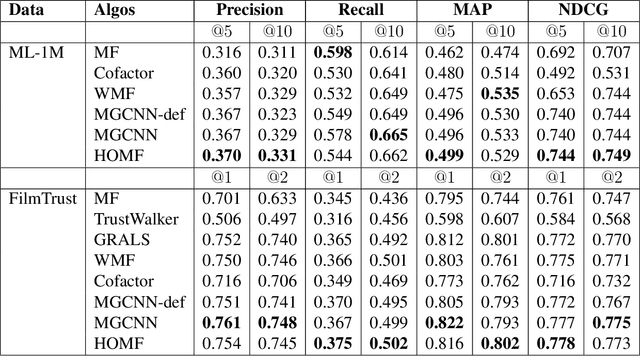
Predicting unobserved entries of a partially observed matrix has found wide applicability in several areas, such as recommender systems, computational biology, and computer vision. Many scalable methods with rigorous theoretical guarantees have been developed for algorithms where the matrix is factored into low-rank components, and embeddings are learned for the row and column entities. While there has been recent research on incorporating explicit side information in the low-rank matrix factorization setting, often implicit information can be gleaned from the data, via higher-order interactions among entities. Such implicit information is especially useful in cases where the data is very sparse, as is often the case in real-world datasets. In this paper, we design a method to learn embeddings in the context of recommendation systems, using the observation that higher powers of a graph transition probability matrix encode the probability that a random walker will hit that node in a given number of steps. We develop a coordinate descent algorithm to solve the resulting optimization, that makes explicit computation of the higher order powers of the matrix redundant, preserving sparsity and making computations efficient. Experiments on several datasets show that our method, that can use higher order information, outperforms methods that only use explicitly available side information, those that use only second-order implicit information and in some cases, methods based on deep neural networks as well.

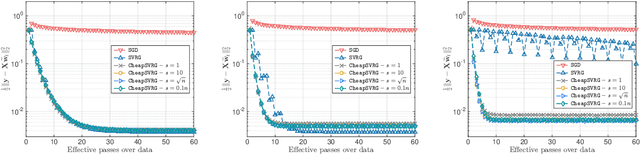
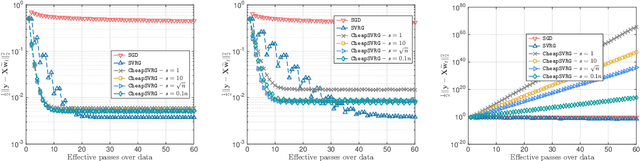
Trading-off variance and complexity in stochastic gradient descent

Stochastic gradient descent is the method of choice for large-scale machine learning problems, by virtue of its light complexity per iteration. However, it lags behind its non-stochastic counterparts with respect to the convergence rate, due to high variance introduced by the stochastic updates. The popular Stochastic Variance-Reduced Gradient (SVRG) method mitigates this shortcoming, introducing a new update rule which requires infrequent passes over the entire input dataset to compute the full-gradient. In this work, we propose CheapSVRG, a stochastic variance-reduction optimization scheme. Our algorithm is similar to SVRG but instead of the full gradient, it uses a surrogate which can be efficiently computed on a small subset of the input data. It achieves a linear convergence rate ---up to some error level, depending on the nature of the optimization problem---and features a trade-off between the computational complexity and the convergence rate. Empirical evaluation shows that CheapSVRG performs at least competitively compared to the state of the art.