Minimum norm solutions do not always generalize well for over-parameterized problems

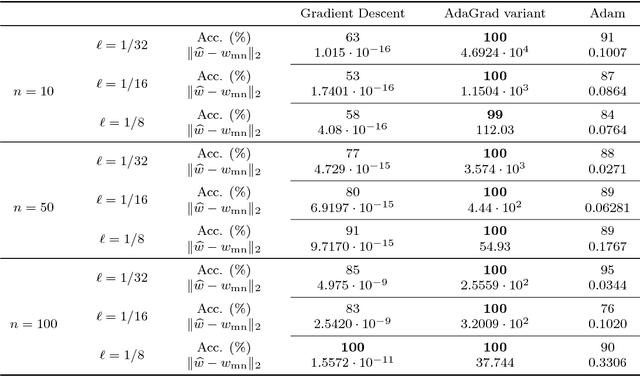
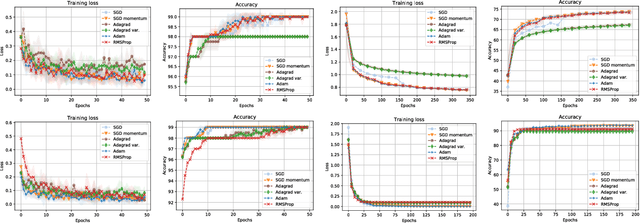
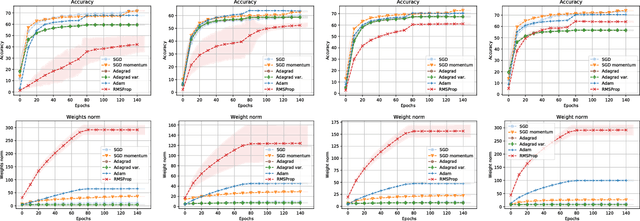
Stochastic gradient descent is the de facto algorithm for training deep neural networks (DNNs). Despite its popularity, it still requires fine hyper-parameter tuning in order to achieve its best performance. This has led to the development of adaptive methods, that claim automatic hyper-parameter tuning. Recently, researchers have studied both algorithmic classes via thoughtful toy problems: e.g., for over-parameterized linear regression, [1] shows that, while SGD always converges to the minimum-norm solution (similar to the case of the maximum margin solution in SVMs that guarantees good prediction error), adaptive methods show no such inclination, leading to worse generalization capabilities. Our aim is to study this conjecture further. We empirically show that the minimum norm solution is not necessarily the proper gauge of good generalization in simplified scenaria, and different models found by adaptive methods could outperform plain gradient methods. In practical DNN settings, we observe that adaptive methods often perform at least as well as SGD, without necessarily reducing the amount of tuning required.