Doppelgänger's Watch: A Split Objective Approach to Large Language Models

In this paper, we investigate the problem of "generation supervision" in large language models, and present a novel bicameral architecture to separate supervision signals from their core capability, helpfulness. Doppelg\"anger, a new module parallel to the underlying language model, supervises the generation of each token, and learns to concurrently predict the supervision score(s) of the sequences up to and including each token. In this work, we present the theoretical findings, and leave the report on experimental results to a forthcoming publication.

Robust Estimation of Tree Structured Markov Random Fields

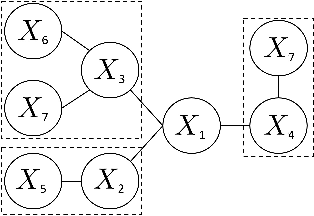
We study the problem of learning tree-structured Markov random fields (MRF) on discrete random variables with common support when the observations are corrupted by unknown noise. As the presence of noise in the observations obfuscates the original tree structure, the extent of recoverability of the tree-structured MRFs under noisy observations is brought into question. We show that in a general noise model, the underlying tree structure can be recovered only up to an equivalence class where each of the leaf nodes is indistinguishable from its parent and siblings, forming a leaf cluster. As the indistinguishability arises due to contrived noise models, we study the natural k-ary symmetric channel noise model where the value of each node is changed to a uniform value in the support with an unequal and unknown probability. Here, the answer becomes much more nuanced. We show that with a support size of 2, and the binary symmetric channel noise model, the leaf clusters remain indistinguishable. From support size 3 and up, the recoverability of a leaf cluster is dictated by the joint probability mass function of the nodes within it. We provide a precise characterization of recoverability by deriving a necessary and sufficient condition for the recoverability of a leaf cluster. We provide an algorithm that recovers the tree if this condition is satisfied, and recovers the tree up to the leaf clusters failing this condition.

Robust Estimation of Tree Structured Ising Models

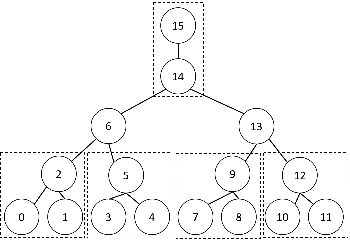
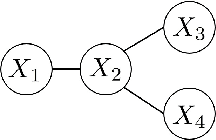
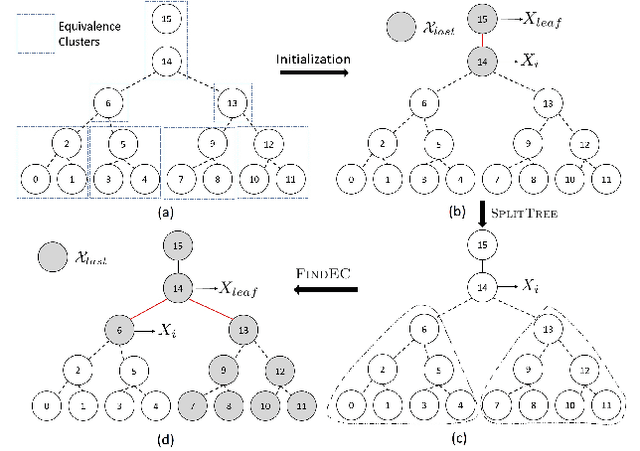
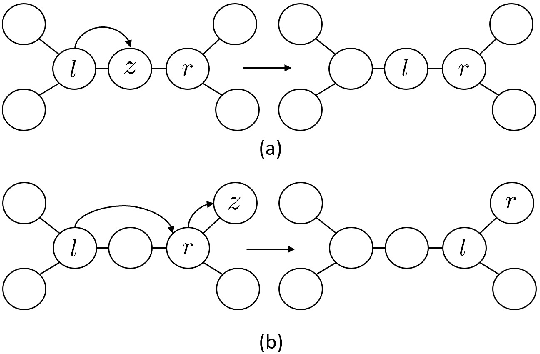
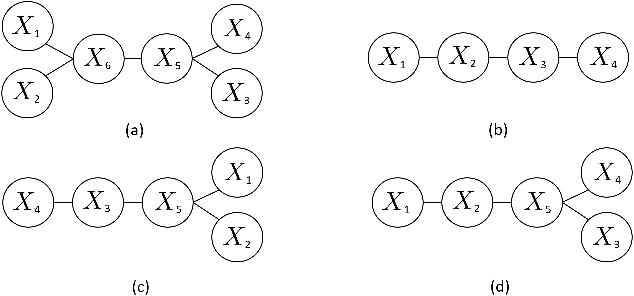
We consider the task of learning Ising models when the signs of different random variables are flipped independently with possibly unequal, unknown probabilities. In this paper, we focus on the problem of robust estimation of tree-structured Ising models. Without any additional assumption of side information, this is an open problem. We first prove that this problem is unidentifiable, however, this unidentifiability is limited to a small equivalence class of trees formed by leaf nodes exchanging positions with their neighbors. Next, we propose an algorithm to solve the above problem with logarithmic sample complexity in the number of nodes and polynomial run-time complexity. Lastly, we empirically demonstrate that, as expected, existing algorithms are not inherently robust in the proposed setting whereas our algorithm correctly recovers the underlying equivalence class.

Robust estimation of tree structured Gaussian Graphical Model

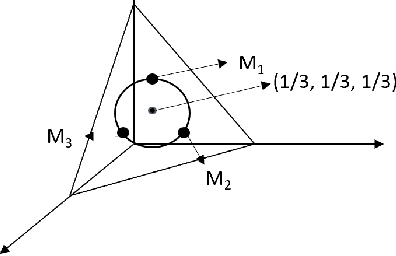
Consider jointly Gaussian random variables whose conditional independence structure is specified by a graphical model. If we observe realizations of the variables, we can compute the covariance matrix, and it is well known that the support of the inverse covariance matrix corresponds to the edges of the graphical model. Instead, suppose we only have noisy observations. If the noise at each node is independent, we can compute the sum of the covariance matrix and an unknown diagonal. The inverse of this sum is (in general) dense. We ask: can the original independence structure be recovered? We address this question for tree structured graphical models. We prove that this problem is unidentifiable, but show that this unidentifiability is limited to a small class of candidate trees. We further present additional constraints under which the problem is identifiable. Finally, we provide an O(n^3) algorithm to find this equivalence class of trees.