Robust Estimation of Tree Structured Ising Models
Paper and Code
Jun 10, 2020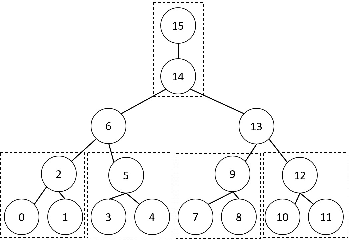

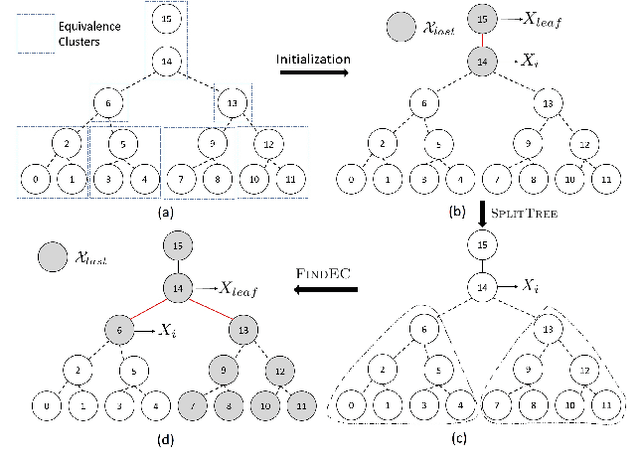
We consider the task of learning Ising models when the signs of different random variables are flipped independently with possibly unequal, unknown probabilities. In this paper, we focus on the problem of robust estimation of tree-structured Ising models. Without any additional assumption of side information, this is an open problem. We first prove that this problem is unidentifiable, however, this unidentifiability is limited to a small equivalence class of trees formed by leaf nodes exchanging positions with their neighbors. Next, we propose an algorithm to solve the above problem with logarithmic sample complexity in the number of nodes and polynomial run-time complexity. Lastly, we empirically demonstrate that, as expected, existing algorithms are not inherently robust in the proposed setting whereas our algorithm correctly recovers the underlying equivalence class.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge